games101系列(3) 光照和纹理
前言
前面两个作业内容以后,我们已经掌握了简单的几何变换以及光栅化过程,现在可以将一个物体和摄像机移动到任意位置,投影得到屏幕坐标,然后通过光栅化与深度测试,计算屏幕上每个像素的值,从而将物体显示到屏幕上。现在,我们再考虑一下真实感,显然颜色是我们忽略的,物体也没有什么阴影,在作业3中,我们使用纹理和光照模型,渲染一个obj对象。着色(Shading),给每个像素一个确定的颜色表示,让物体显示出明暗特征;纹理,让物体表面呈现不同的性质(凹凸,颜色等)。之前的作业中,我们都是用的黑白颜色来表示物体。
现在,我们先介绍Blinn-Phong反射模型,这是一种简单的光照模型;然后再看看纹理技术的实现,最后在作业中将这些方法全部实现。
Blinn—Phong Reflectance Model
通过观察光照下的一个光滑物体表面(下面的茶杯),这种模型将物体上的光分为三种类。
- Specular highlights,镜面光,是物体上最亮的那部分高光;
- Diffuse reflection,漫反射光,是物体上渐变的那部分光,在面对光源的地方让物体显得比较明亮,背对光源的地方让物体显得比较暗淡;
- Ambient lighting,环境光,环境中其他物体反射到茶杯上的光;
通过这三种类型的光,就能简单地模拟光照情况。现在从数学角度介绍一下这几种光的计算方法。
Diffuse reflection
显然,这种光出现的地方应该和物体与光源的角度有关。正对光源就应该比较亮,否则就比较暗。所以我们先定义几个方向向量,然后在此基础上具体计算。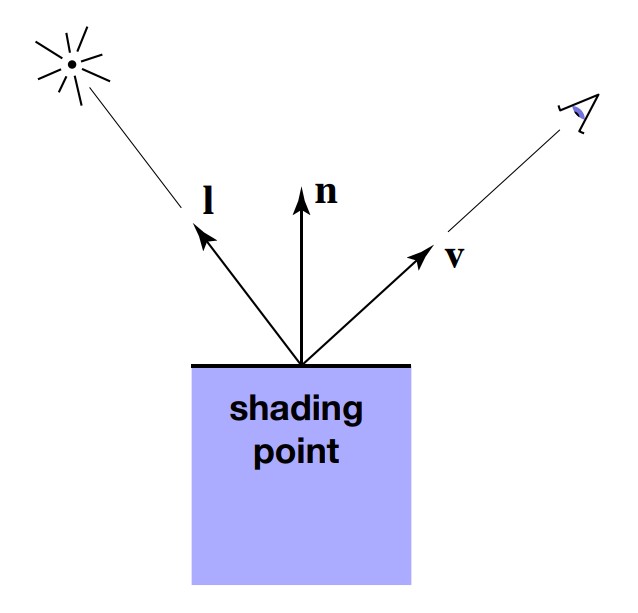
l是从待着色点指向光源的单位向量,n是待着色点在物体表面的法线向量,b则是从待着色点指向摄像机的单位向量。初次之外,还做一种假设,一个点光源朝四面八方发出光线,能量会逐渐衰减,这里假设能量与离光源的距离的平方成反比。最后得到这样的式子,被称为Lambert’s law: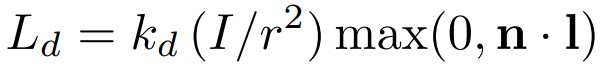
其中 Ld 是待着色点光强,Kd 是漫反射系数,决定物体接受光照以后是什么颜色;I 表示点光源的能量,r 表示距离;最后一项决定光源以这种角度照射到着色点,会接受多少能量,且这个值不会为负数,否则后方照来的光线也会照亮待着色点。
漫反射光的位置与摄像机视角无关,只和光源与物体表面法线的夹角有关。
Specular highlights
从直觉上感受,镜面光应该与摄像机视角有关了,从光学上解释,这部分光是光源的光线反射出来的,包含了大部分的能量,所以比较明亮。
通过反射,我们定义一个半程向量h,也就是向量l和v的角平分线向量。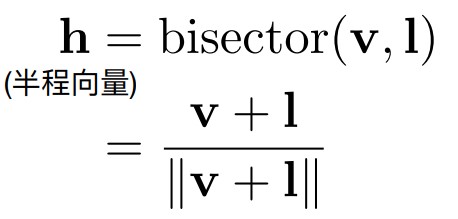
之所以使用这个向量,是因为我们假设当观察视角和反射光方向比较接近的时候,看到的镜面光比较强;而这个时候,角平分线向量就应该比较接近法线向量,也就是直接比较法线向量n和这个半程向量就可以得出光照结果了,避免了反射光的复杂计算。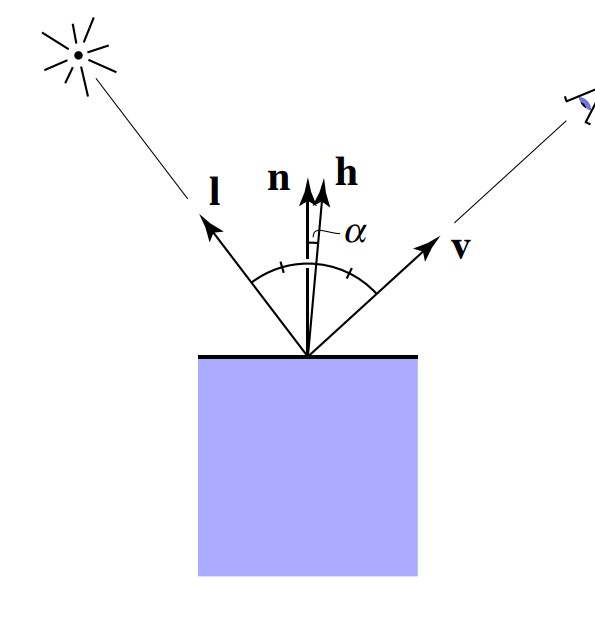
然后和漫反射相似,也定义一个镜面反射系数 Ks, 另外还引入一个容忍度 p。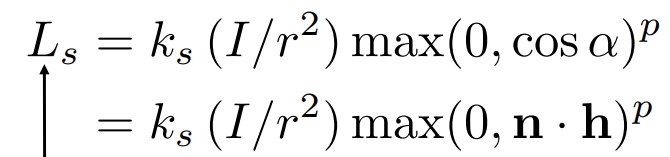
由于后一项一定是在[0,1]之间的值,所以容忍度p越大,随着夹角变大,该项下降地就越快,镜面光就越暗,也就是容忍度与镜面光面积大小成反比。
Ambient lighting
由于是环境光,所以从任何方向观察都应该没有变化,而且还不和光源有关系,换句话说这种光应该是常数项。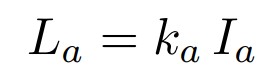
Ka 是环境光反射系数,Ia则是环境光强度。
总结
现在我们将三种光加起来,这就是Blinn-Phong反射模型的效果。不过要注意,这种光照模型是各向同性的,如果固定视角和光源,旋转物体,得到的效果完全一样,因此不适用于各向异性材质。
着色频率
Flat Shading 平面着色
这种着色方式对每个三角形进行一次着色,每个面计算一个法线向量。
Gouraud Shading 顶点着色
对每个顶点进行一次着色,以插值的方式计算所有点的颜色。
这样一来每个顶点都需要一个法线,使用每个顶点相邻面的法线和的平均值(例如加权和平均)。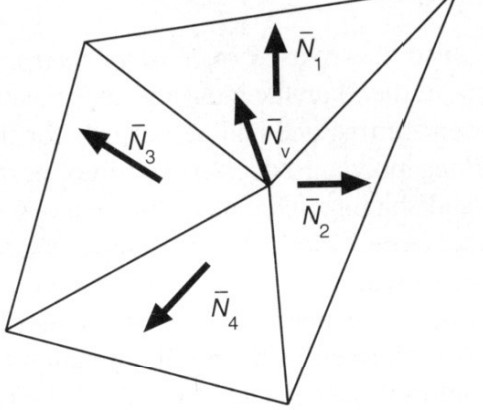
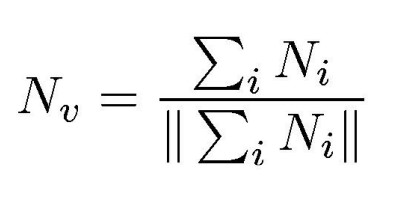
Phong Shading 像素着色
这种着色方式并不是前面提到的光照模型,对每个像素计算一个法线,方法就是先计算每个顶点的法线,然后利用重心坐标,求出三角形内部的所有像素的法线。
实时渲染管线
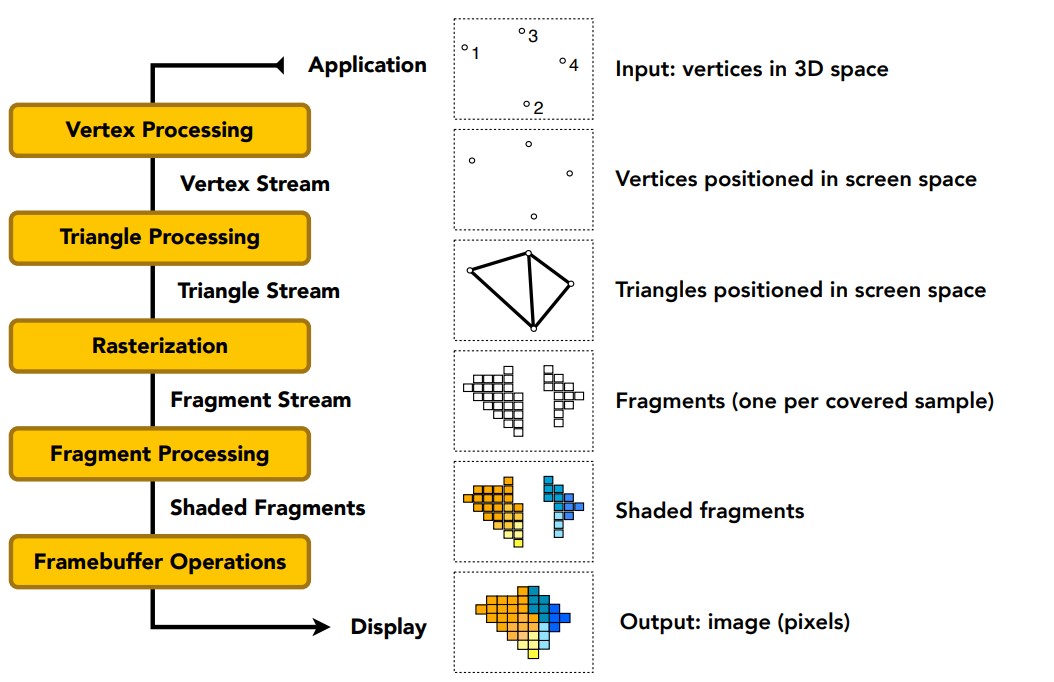
现在可以好好总结渲染管线了,首先我们定义一系列顶点,以及这些顶点的连接方式,从而构成一个物体。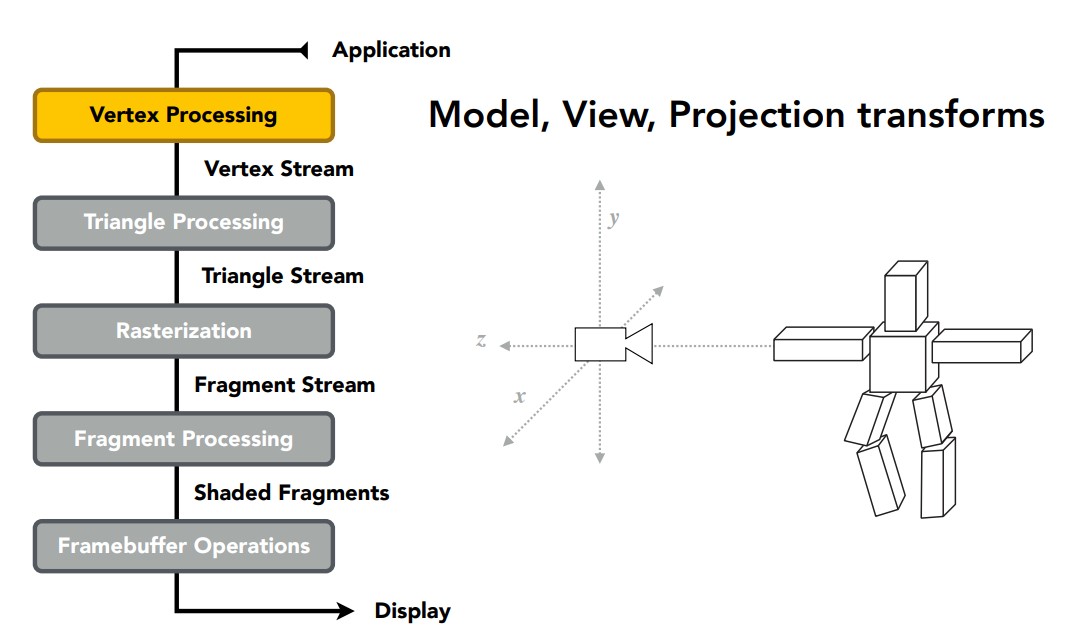
然后对这些顶点流斤进行MVP变换,移动到我们想要的位置。确定以后,按照连接方式连接这些顶点,形成三角形流。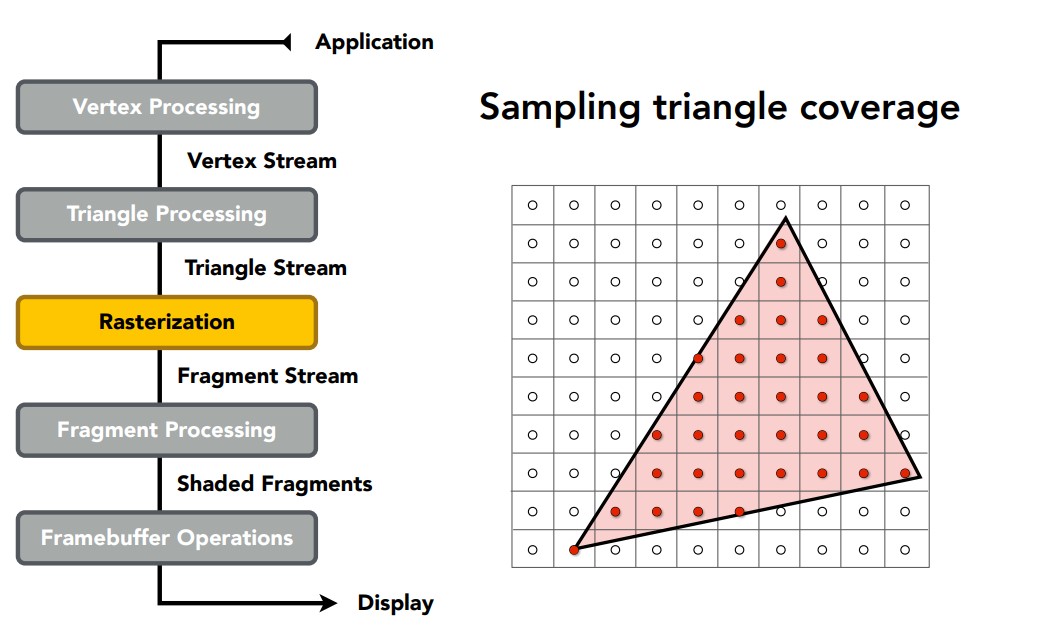
接着像素在许多三角形上进行采样,判断内部外部,生成片段流。这里的片段流指的是一个采样点覆盖的区域,例如一个像素采样一次就是一个片段,一个像素如果有四个子像素采样就是四个片段。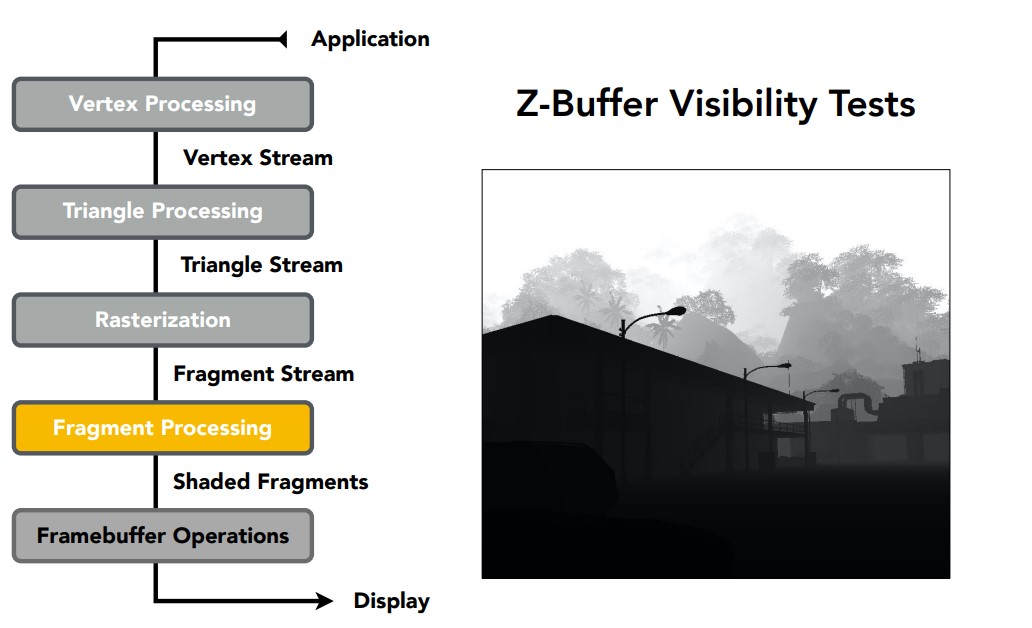
进行深度测试,用Z-Buffer判断不同片段的可见性。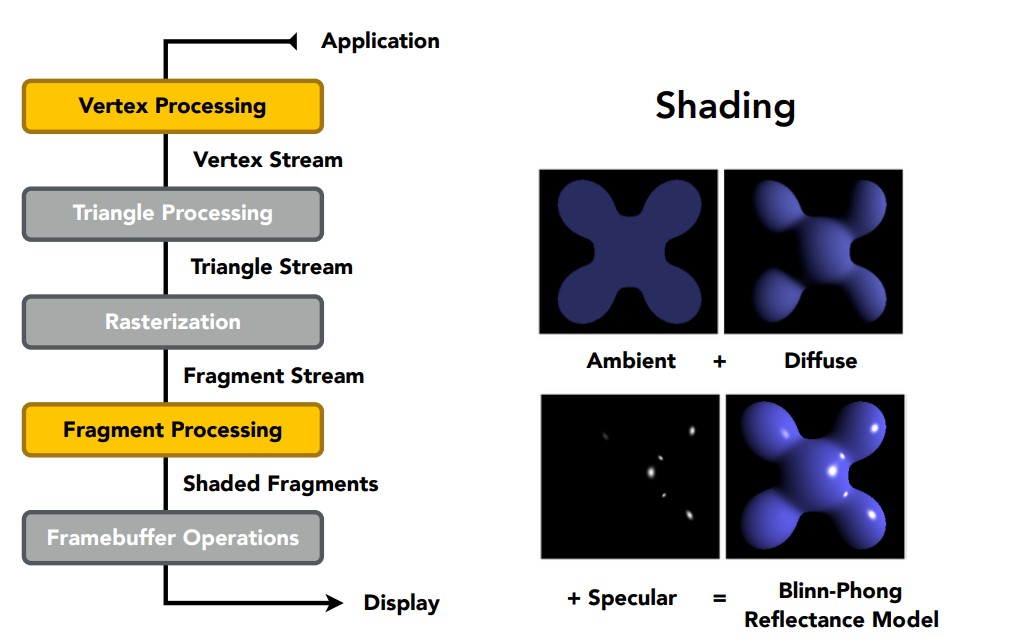
完成后光照模型也在这里应用,依然对可见的片段流处理。通过插值求出片段流的法线向量。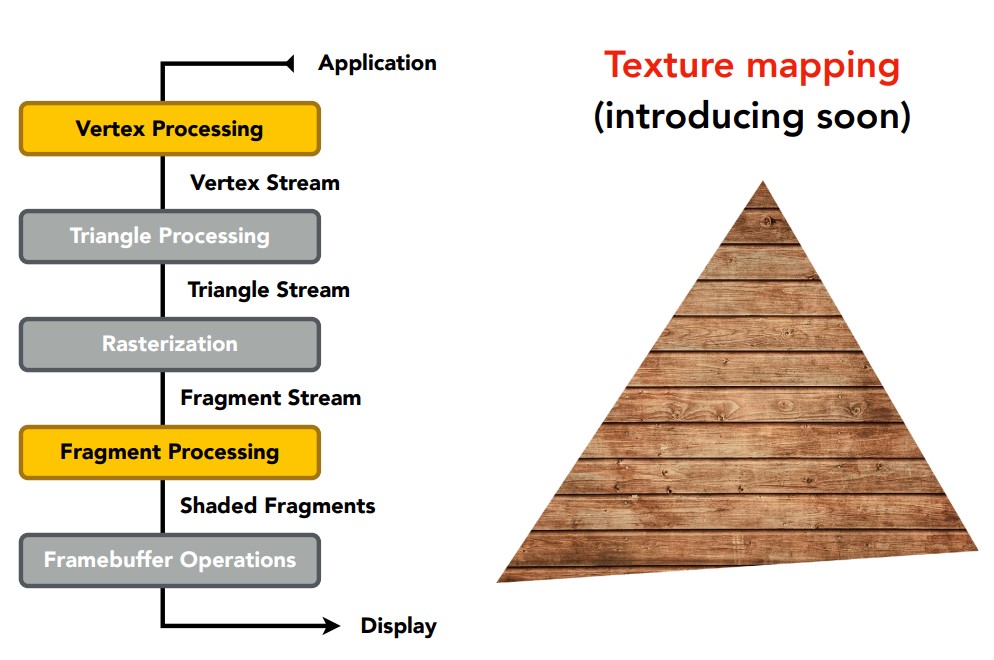
纹理操作同样对片段进行处理,这部分后面再介绍。
根据处理对象的不同,各种计算也发生在不同的阶段,例如对顶点进行几何变换就是顶点处理阶段发生的,规定三角形法线自然也要到三角形处理阶段完成,反比后面计算顶点法线,甚至进行插值。当然不同的API有不同的渲染管线定义,大致和这个类似,也不用完全依照这个记忆,重在理解。
纹理映射
物体上如果通过手动指定的方式实现各种细节,需要的数据量是非常大的,所以采用纹理进行辅助,让物体上的一个点能够通过查询的方式找到它对应的属性,这个属性可以是颜色,也可以是几何特点,还可以是其他特征。
而纹理函数通常是二维的函数,定义纹理坐标(u,v)用来查询纹理上的值,纹理坐标又对应实际渲染像素(i,j),通过某种方式将像素(或者说片段)的坐标映射到纹理坐标,查询需要的特征,就是纹理映射的过程。
像素放大
纹理分辨率过小,导致纹理映射的纹理坐标出现非整数值,所以需要将纹理放大。这里有三种放大纹理的方法,Nearst,Bilinear,Bicubic。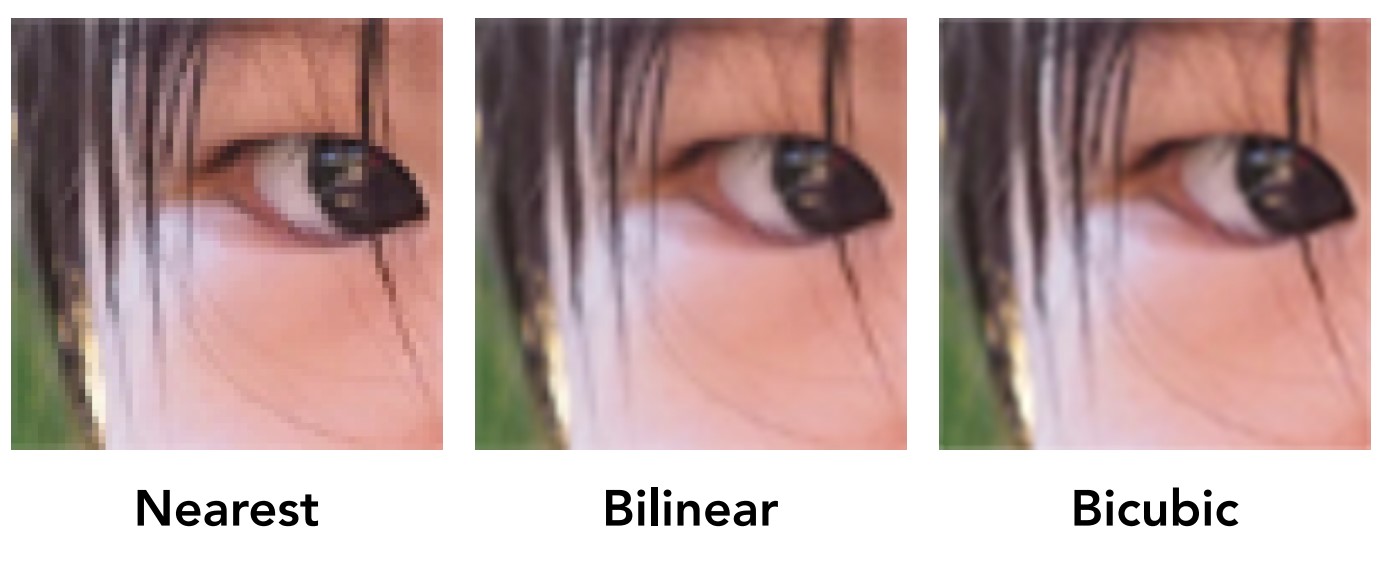
Nearst,根据纹理坐标取最近的整数值,即四舍五入,不过这样导致不同的纹理查询到相同的颜色。
Bilinear,双线性插值,在u,v方向上先选择一个方向进行线性插值,然后再使用插值结果在另外一个方向进行线性插值,就是双线性插值。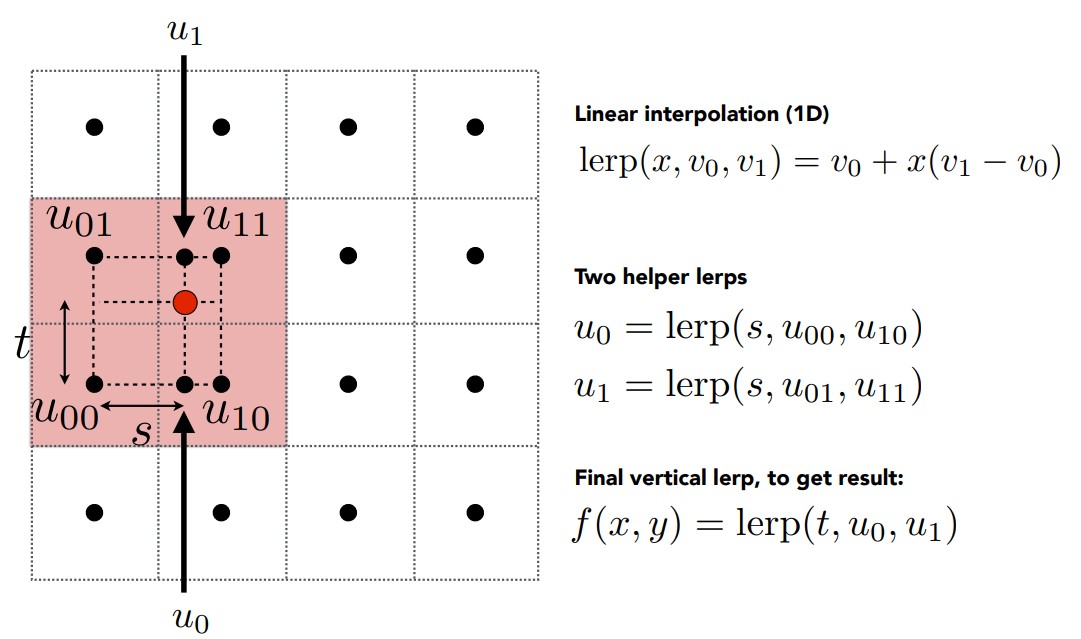
如图先选择水平u方向插值,得到u0和u1,然后用u1和u0的垂直v方向插值,得到目标点的颜色值。
Bicubic,和双线性插值类似,不过取16个相邻的纹理颜色而不是4个进行插值。
像素缩小
纹理分辨率过大,查询的时候一个像素可能对应多个纹理值,应该缩小纹理。提高采样频率可以解决,例如前面的MSAA,但是太耗费时间。
MipMap
采用范围查询代替点查询,具体做法是使用Mipmap,不断对一个纹理进行区域平均(平均一定大小块的颜色值)。
但是怎么确定查询那个维度等级的MipMap呢?首先我们知道,维度每上升一次,纹理大小就缩小一倍,因此我们要找到这个缩放的比例,就先定义一个距离L,在一个像素查询纹理的同时,查询它相邻两个像素的纹理坐标,通过这三个纹理坐标计算L如下: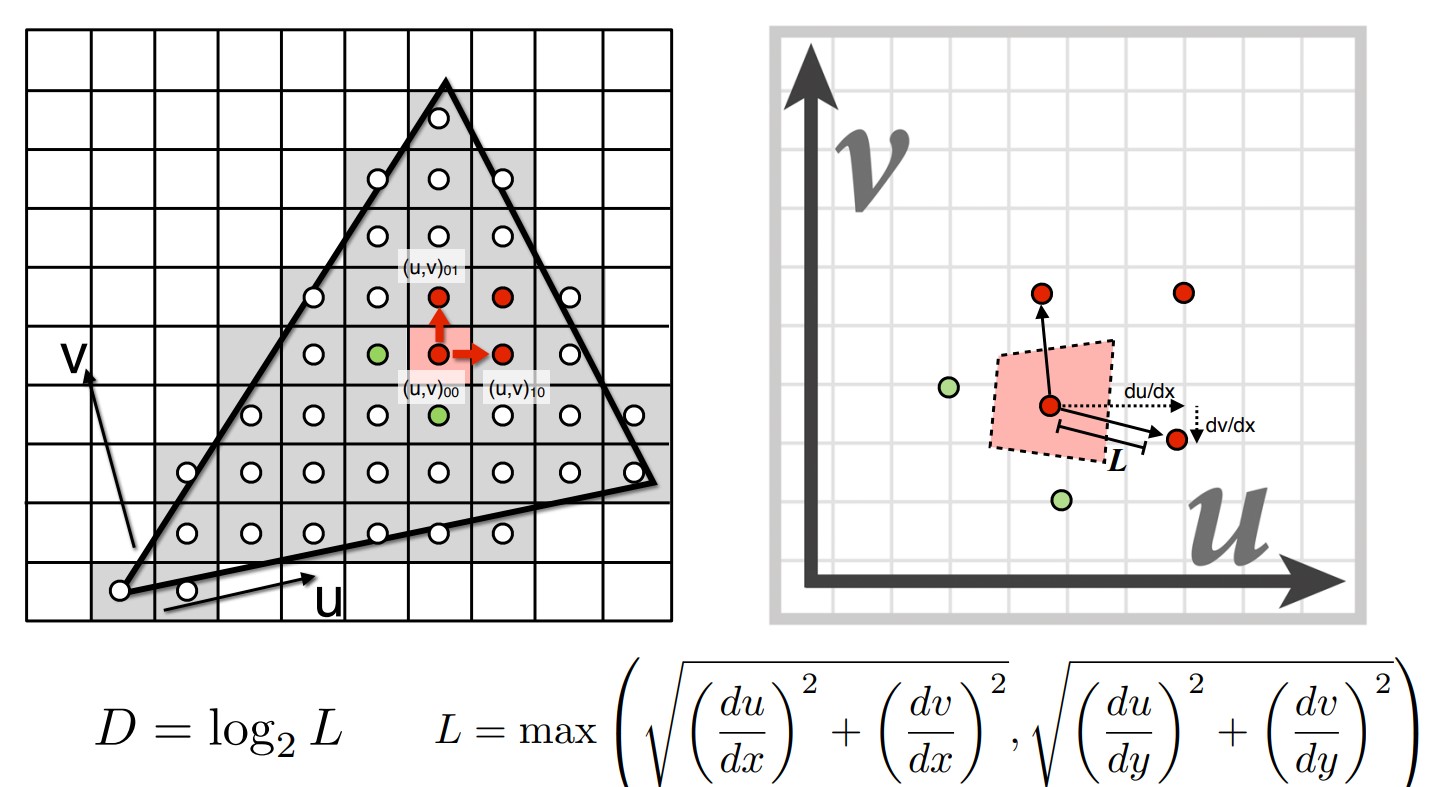
然后直接对L取对数,找到缩小多少倍,就得到维度D了。当然D可能不是整数,需要进一步处理。如果直接四舍五入,得到的纹理显然不连续。
三线性插值
对于D不是正数的情况,当然还可以通过插值解决。在D的两个上下界维度的MipMap中,分别做双线性插值,找到两个对应的纹理特征,再用这两个特征在MipMap维度上插值。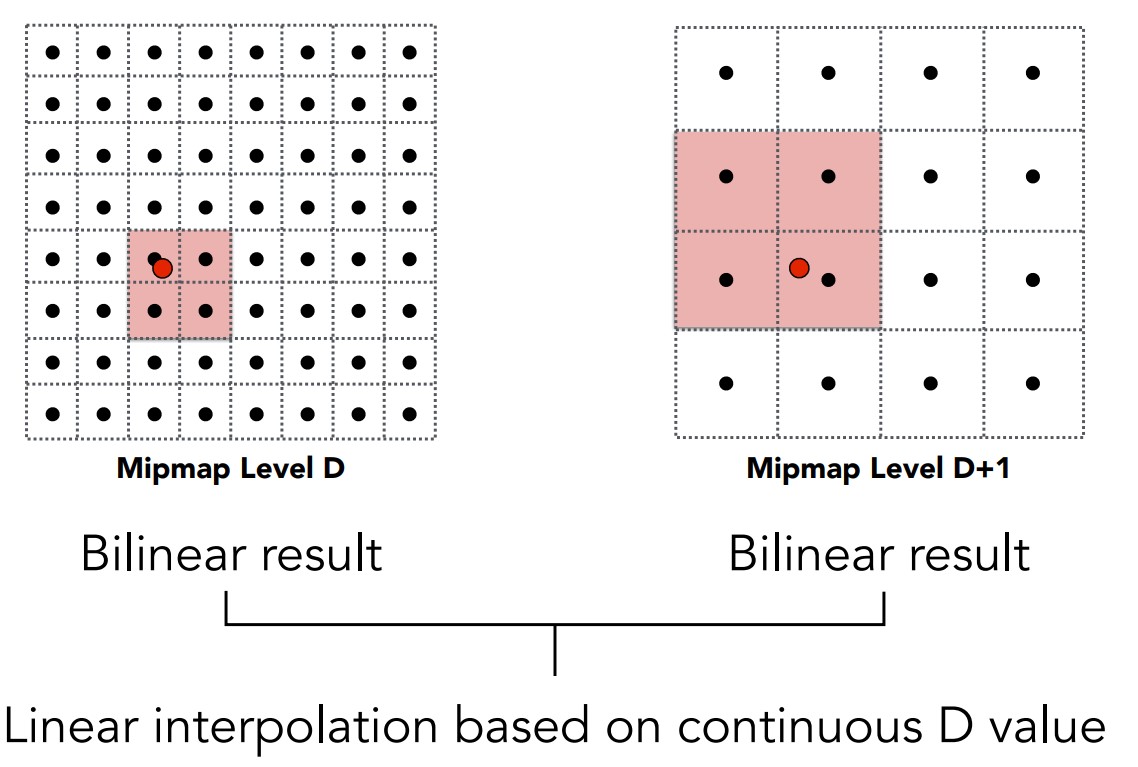
通过这样的方式查新一个像素的纹理,整个图形得到的纹理特征就显然是连续的了。
各向异性
现在看看MipMap处理后的结果图形。
这是直接采样的结果。
通过上面的MipMap得到的结果,在远处的图形还是变得模糊了,这是因为MipMap处理的仅是正方形,前面进行距离L计算的时候,取像素邻居模拟的是一个正方形形状,但是有时候映射到纹理图上这个像素邻居组成的矩形并不是正方形,而是矩形或其他形状。而且,三线性插值本来也是一种近似处理,所以得到的结果显然没有那么精细。
解决的方法就是使用各向异性过滤,可以设置将MipMap在水平或竖直方向进行压缩,从而解决映射结果为水平矩形或者竖直矩形的问题。但是对于斜的矩形,仍然效果不好,可以使用EWA过滤解决,这里不再讨论。
应用
环境光贴图 Environment Map
用贴图记录各个方向的光照,表示环境光。
凹凸贴图 Bump Mapping
记录顶点法线的偏移,但是不改变物体原本的几何信息。查询到纹理坐标后,先求该坐标在凹凸曲线上的法线(通过导数),然后再垂直并取单位值得到法线向量。图中h表示高度函数,C表示扰动程度。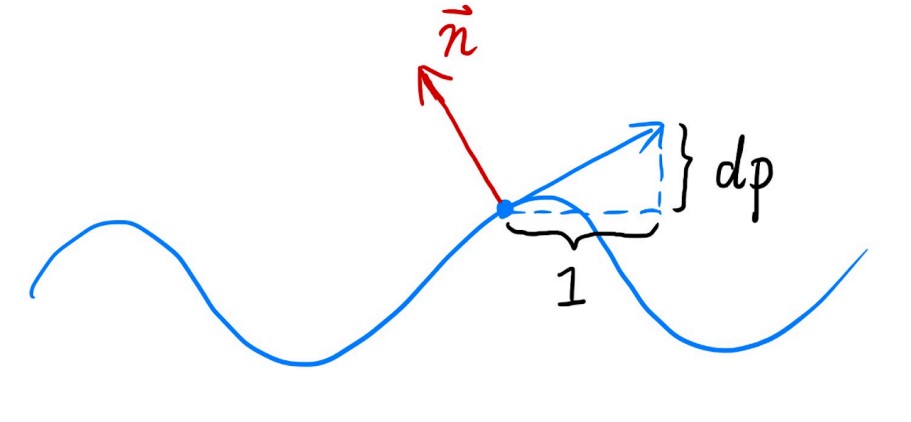

三维的情况,先求其中两个方向的切线,然后同样垂直得到结果。
位移贴图 Displacement mapping
使用和凹凸贴图相同的原理,不过会使得顶点实际发生移动。凹凸贴图和位移贴图会在作业中实现。
程序化纹理 Procedural Noise&Procedural textures
定义一种噪声函数作为纹理来进行查询。
预计算着色 Precomputed Shading
纹理存储环境光遮蔽的信息,着色的时候使用其他着色结果与这个信息作用,得到结果。
3D Texture and Volume rendering
纹理是三维的,应用在体积渲染中。
作业3
作业3的内容比较多,在这次作业中实现了一个完整的渲染框架,包括前面的变换,以及这次的光照纹理,一共实现了五种渲染,使用法线作为颜色的Normal,使用Phong光照模型的Phong,应用了纹理的Texture,使用了凹凸贴图并且以法线作为颜色的Bump,最后应用了位移贴图的Displacement,要编写的就是这些shader,其中第一个shader已经给出。
投影矩阵
使用前面编写的函数即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
// TODO: Use the same projection matrix from the previous assignments
// Students will implement this function
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
Eigen::Matrix4f M_p_o, M_scale, M_translate;
//计算视锥
float top, bottom, left, right, near, far, fovY;
fovY = eye_fov / 180 * PI;
near = -zNear;
far = zFar;
top = tan(fovY / 2) * zNear;
bottom = -top;
right = top * aspect_ratio;
left = -right;
//计算矩阵
M_scale << 2 / (right - left), 0, 0, 0,
0, 2 / (top - bottom), 0, 0,
0, 0, 2 / (near - far), 0,
0, 0, 0, 1;
M_translate <<
1, 0, 0, -(right + left) / 2,//==0
0, 1, 0, -(top + bottom) / 2,//==0
0, 0, 1, -(near + far) / 2,//!=0
0, 0, 0, 1;
M_p_o << near, 0, 0, 0,
0, near, 0, 0,
0, 0, near + far, -near * far,
0, 0, 1, 0;
projection = M_scale * M_translate * M_p_o * projection;
return projection;
}
Normal
第一个模型由于shader已经给出,现在反而要求是编写片段的各种插值量,修改第二次作业的光栅化函数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos)
{
// TODO: From your HW3, get the triangle rasterization code.
auto v = t.toVector4();//返回顶点的齐次坐标形式
// TODO : Find out the bounding box of current triangle.
int box_l, box_r, box_b, box_t;
box_l = static_cast<int> (std::min(v[0].x(), std::min(v[1].x(), v[2].x())));
box_r = static_cast<int> (std::max(v[0].x(), std::max(v[1].x(), v[2].x())));
box_b = static_cast<int> (std::min(v[0].y(), std::min(v[1].y(), v[2].y())));
box_t = static_cast<int> (std::max(v[0].y(), std::max(v[1].y(), v[2].y())));
std::vector<Eigen::Vector2f> position{
{0.25, 0.25},
{0.75, 0.25},
{0.25, 0.75},
{0.75, 0.75}
};
// iterate through the pixel and find if the current pixel is inside the triangle
for (int i = box_l; i <= box_r; i++)
{
for (int j = box_b; j <= box_t; j++)
{
int count = 0;
for (int index = 0; index < 4; index++)
{
if (insideTriangle(position[index].x() + i, position[index].y() + j, t.v))
count++;
}
// If so, use the following code to get the interpolated z value.
if (count > 0)
{
// TODO: Inside your rasterization loop:
// * v[i].w() is the vertex view space depth value z.
// * Z is interpolated view space depth for the current pixel
// * zp is depth between zNear and zFar, used for z-buffer
float alpha, beta, gamma;
std::tie(alpha, beta, gamma) = computeBarycentric2D(static_cast<float>(i + 0.5), static_cast<float>(j + 0.5), t.v);
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;
if (depth_buf[get_index(i, j)] > -zp)
{
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
depth_buf[get_index(i, j)] = -zp;
//插值求颜色,法线,纹理坐标,着色坐标
// TODO: Interpolate the attributes:
// auto interpolated_color
// auto interpolated_normal
// auto interpolated_texcoords
// auto interpolated_shadingcoords
auto interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1);
auto interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1).normalized();
auto interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1);
auto interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1);
// Use: Instead of passing the triangle's color directly to the frame buffer, pass the color to the shaders first to get the final color;
fragment_shader_payload payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
Eigen::Vector2i point;
point << i, j;
set_pixel(point, pixel_color * (count / 4.0));
}
}
}
}
}
修改一个是上面几项插值计算,颜色,法线,纹理坐标,着色坐标(着色器要用),计算出重心坐标以后用函数即可。另外还有一个改动是set_pixel,作业二中传入的point三维坐标改成了二维,因为像素只用XY坐标。最后注释给出Z轴插值坐标计算,与作业二相比改了一下名字。
实际上必要的代码都给了,但是需要调整代码,不然写完这个函数以后用Normal着色器很可能会报错,多修改几次。
Phong
现在开始,就可以正式编写shader了。首先看看给出的法线着色器例子,熟悉一下传入的参数是什么。1
2
3
4
5
6
7Eigen::Vector3f normal_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = (payload.normal.head<3>().normalized() + Eigen::Vector3f(1.0f, 1.0f, 1.0f)) / 2.f;
Eigen::Vector3f result;
result << return_color.x() * 255, return_color.y() * 255, return_color.z() * 255;
return result;
}
分析代码,payload包含了片段的颜色、法线,纹理坐标、顶点转换到视角坐标系中的坐标信息,这个着色器中将片段的法线坐标归一化后加上0.5,然后放大到255的颜色值,返回就构成了上面的颜色结果,还是比较好看的。
根据前面介绍的理论,Phong反射光照模型可以用一个公式表示片段颜色,框架中也给了模型中一些值的取值,要做的只是用这些值,在循环中分别计算不同的光照效果,然后相加。注意环境光由于不会改变,所以可以放在循环体外。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f v = (eye_pos - point).normalized();
Eigen::Vector3f h = (l + v).normalized();
float r = (light.position - point).dot(light.position - point);
//diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r) * std::max(0.0f, normal.dot(l));
//specular
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r) * std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += Ls + Ld;
}
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
result_color += La;
return result_color * 255.f;
}
首先规定了三种光的反射系数(反射光和总光能量的比例),其中漫反射就是直接采用在前面插值计算出的颜色,作为物体表面的颜色。然后规定了两个光源,指定了位置和强度(对应RGB分量强度),确定了摄像机位置,环境光颜色。然后再次规定了片段坐标point,片段法线normal,结合前面规定的光源位置和摄像机位置,还有物体在视点坐标系中的坐标,就可以用这个循环计算两个光源的效果了。
循环里面,计算理论部分定义的l,v,h向量判断光照情况,然后就是公式计算,得到结果颜色后仍然是归一化的结果,放大到255的颜色区间。这样,就完成了一个着色器,不过我看到网上有人说,将环境光计算放到循环里会导致画面变暗,应该是result_color加了两次环境光,环境光有比较暗的情况,导致归一化的结果也变暗了。完成后是下面这个样子。
Texture
现在在上面光照模型的基础上,还要加上纹理的应用。原理就是修改光照模型的漫反射颜色,其他完全相同。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = {0, 0, 0};
if (payload.texture)
{
// TODO: Get the texture value at the texture coordinates of the current fragment
return_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());
}
Eigen::Vector3f texture_color;
texture_color << return_color.x(), return_color.y(), return_color.z();
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = texture_color / 255.f;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = texture_color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f v = (eye_pos - point).normalized();
Eigen::Vector3f h = (l + v).normalized();
float r = (light.position - point).dot(light.position - point);
//diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r) * std::max(0.0f, normal.dot(l));
//specular
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r) * std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += Ls + Ld;
}
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
result_color += La;
return result_color * 255.f;
}
实际上,纹理坐标和纹理都已经给到片段的payload中了,而且方法也写好,向上面那样调用,会得到一个三维的颜色值,作为漫反射系数,然后进入Phong反射模型计算颜色即可。
凹凸贴图
知道纹理的基本用法,现在考虑一下凹凸贴图的原理,需要计算微分求切线,微分量取纹理宽度或高度的倒数,然后垂直得到法线向量。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement bump mapping here
// Let n = normal = (x, y, z)
float x = normal.x();
float y = normal.y();
float z = normal.z();
Vector3f t(x * y / sqrt(x * x + z * z), sqrt(x * x + z * z), z * y / sqrt(x * x + z * z));
Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
//TBN矩阵的作用是将局部坐标转化成实际坐标表示
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
//求u,v微分
float dU = kh * kn * (payload.texture->getColor(u + 1 / w, v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln(-dU, -dV, 1);
Eigen::Vector3f result_color = (TBN * ln).normalized();
return result_color * 255.f;
}
注释中写出了大部分伪代码,但是这里还是要说明,凹凸贴图的计算涉及到TBN矩阵和切空间,可以简单理解为把物体的三维坐标和纹理坐标连接起来,课程中只说了后面求局部坐标系中法线的方法,并且让局部坐标系中的法线都为(0,0,1),这个局部空间实际上就是TBN空间,在u和v方向求切线后得到垂直的扰动法线,当然要将这个纹理空间中的法向量转化到片段所在的空间。所以TBN矩阵就是将局部坐标中的法向量变换到着色时的空间中了。
具体的计算可以找这部分知识推导,理解可以就这样。
位移贴图
在实现了凹凸贴图的基础上,对顶点做实际的移动。所以要添加的代码只有一行。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
float x = normal.x();
float y = normal.y();
float z = normal.z();
Vector3f t(x * y / sqrt(x * x + z * z), sqrt(x * x + z * z), z * y / sqrt(x * x + z * z));
Vector3f b = normal.cross(t);
Eigen::Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
//TBN矩阵的作用是将局部坐标转化成实际坐标表示
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
//求u,v微分,微分量取纹理宽、高的倒数
float dU = kh * kn * (payload.texture->getColor(u + 1 / w, v).norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln(-dU, -dV, 1);
//仅仅添加了下面这一行函数
point = point + kn * normal * payload.texture->getColor(u, v).norm();
normal = (TBN * ln).normalized();
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// TODO: For each light source in the code, calculate what the *ambient*, *diffuse*, and *specular*
// components are. Then, accumulate that result on the *result_color* object.
Eigen::Vector3f l = (light.position - point).normalized();
Eigen::Vector3f v = (eye_pos - point).normalized();
Eigen::Vector3f h = (l + v).normalized();
float r = (light.position - point).dot(light.position - point);
//diffuse
Eigen::Vector3f Ld = kd.cwiseProduct(light.intensity / r) * std::max(0.0f, normal.dot(l));
//specular
Eigen::Vector3f Ls = ks.cwiseProduct(light.intensity / r) * std::pow(std::max(0.0f, normal.dot(h)), p);
result_color += Ls + Ld;
}
Eigen::Vector3f La = ka.cwiseProduct(amb_light_intensity);
result_color += La;
return result_color * 255.f;
}
得到了下面的结果:
总结
到这里作业就全部完成了,提高项这次就不做了,有机会再说。关于代码还要提到一个点,计算result_color的时候,先声明其为一个全0的三维向量,后面赋值只能一次一次累加,而不能直接赋值,例如result_color = Ls + Ld,只能是result_color += Ls + Ld,否则得到的最后这个位移贴图结果就是比较灰暗的,这就是因为有两个光源,直接赋值显然就错了,只计算了一个光的光照结果。