游戏开发经常会问这个问题,因为Unity的导航系统用的是A*算法,并且有时候还需要进一步改进,这里将以这篇文章 为主,介绍几种寻路算法算法。
广度优先 广度优先是最简单的寻路算法了,它从出发点开始,用一个队列存储当前点的邻居点,然后开始迭代,每次出队一个点,再将新点的邻居入队。同时用一个集合存储已经访问过的结点,遍历的时候会跳过这些点避免重复访问。
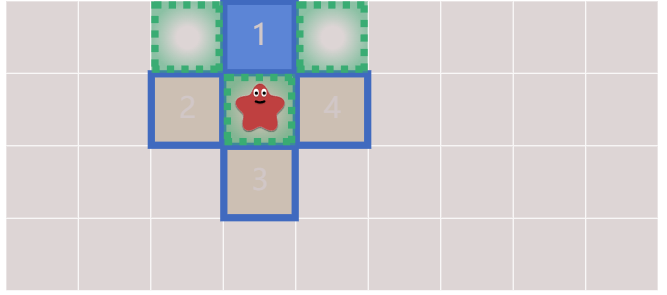
例如上图中,我们从★源点开始,它的四个邻居标号为1,2,3,4,依次添加到队列中并添加到已访问的结点集合里,然后下一次遍历出队1,将上图中绿色的点入队。不过由于源点已经访问过,所以不会再被入队。伪代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 //Declare Queue<int> q; Set<int> s; q.push(start); s.push(start); //Start iteration while(!q.empty()) { current = q.pop(); for(neighbors of current) { if(s.contain(neighbors) == false) { q.push(neighbors); s.push(neighbors); } } }
但是仅仅这样不能找到我们是从哪条路过来的,因为广度优先遍历仅仅是遍历,要想找到路径需要我们进一步手动记录。这里我们修改集合s,让它作为一个哈希表或字典,进一步记录访问过的结点的父结点是谁。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 //Declare Queue<int> q; Hash<int> s; q.push(start); s[start] = None; //Start iteration while(!q.empty()) { current = q.pop(); for(neighbors of current) { if(s.contain(neighbors) == false) { q.push(neighbors); s[neighbors] = current; } } }
这样当我们遍历到终点时,就可以不断回溯这个哈希表,找到这条路径。而且由于一个点只对应一个父结点,因此路径是唯一确定的。我们通过下面的伪代码找到路径:
1 2 3 4 5 6 7 8 9 10 current = goal; path = []; while(current != start) { path.push(current); current = s[current]; } path.push(start); //reverse so that the first element is start path.reverse();
单源单目标寻路 上面我们能找到的是一个点到其它所有点的路径,然而我们其实并不需要这么做,我们只需要找到目标点的路径。因此上面的算法有太多无效计算。当然可以等找到目标点就马上停止,这也是一种改进方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 //Declare Queue<int> q; Hash<int> s; q.push(start); s[start] = None; //Start iteration while(!q.empty()) { current = q.pop(); //Pay attention here if(current == goal) break; for(neighbors of current) { if(s.contain(neighbors) == false) { q.push(neighbors); s[neighbors] = current; } } }
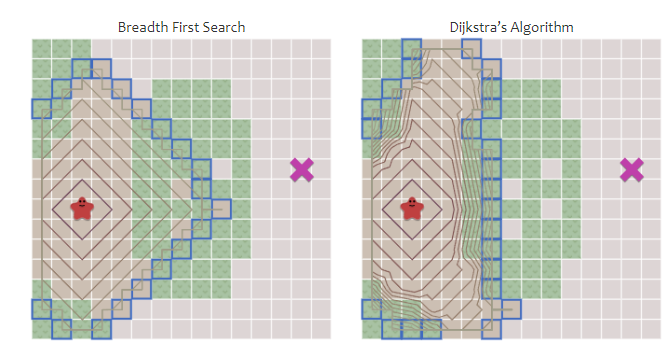
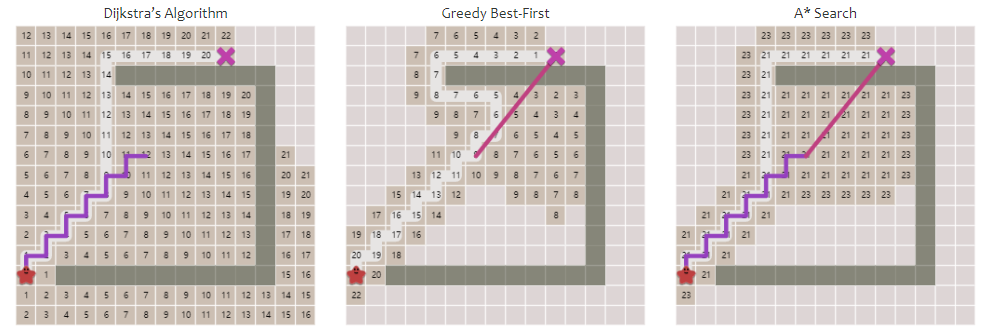
考虑路径花费 现在我们进一步把结点的花费考虑进来,换句话说移动到不同结点的花费是不同的,我们需要找出其中最小的花费。比如文明中,沙漠中移动需要花费一点行动而跨山、森林需要五点。这里我们采用Dijkastra算法,在前面算法的基础上添加一个名为cost的变量来记录当前路径的花费,并且使用优先队列来记录结点。逻辑上也需要改变,不再将所有邻居放入优先队列,还要当这条新的路径优于原本路径时才添加,使得算法不会轻易选择那些花费较大的路径。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 PriorirtQueue<int> q; Hash<int> s; Hash<int> cost; q.push(start); s[start] = None; cost = 0; while(s.empty() == false) { currnet = s.pop(); if(current == goal) break; for(neighbors of current) { //Calculate new cost newcost = cost[current] + graph.cost(neighbors); if(s.contain(neighbors) == false || newcost < cost[neighbors]) { cost[neighbors] = newcost; q.push(neighbors, newcost); s[neighbors] = current; } } }
跟之前的方法相比,现在遍历扩张就考虑了路径代价。注意我们的优先队列出队应返回最小优先级的对象。这可能跟你之前学习的Dijkastra不太像,这里做了一些改变,但是它们都属于一种贪心,即选择当前耗费最少的路径。
启发式方法 启发式指的是人为构造一个公式计算某个数值,这里用来估计当前点到目标点的距离。文章直接使用棋盘距离作为启发式。
1 2 3 4 int heuristic(a,b) { return abs(a.x-b.x) + abs(a.y-b.y); }
我们使用上面的式子修改之前广度优先算法,优先将具有最小估计距离的点拿出来遍历。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 //Declare PriorityQueue<int> q; Hash<int> s; q.push(start); s[start] = None; //Start iteration while(!q.empty()) { current = q.pop(); if(current == goal) break; for(neighbors of current) { if(s.contain(neighbors) == false) { q.push(neighbors, heuristic(goal, next)); s[neighbors] = current; } } }
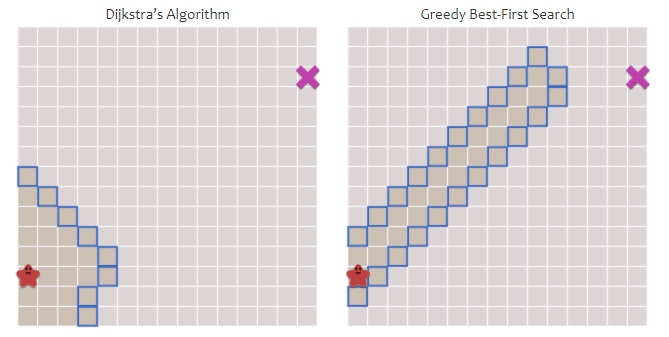
这样路径搜寻会比Dijkastra算法进一步地优先访问距离目标点近的结点,而不是依靠当前的花费决定,我们的方法现在有了目标感。
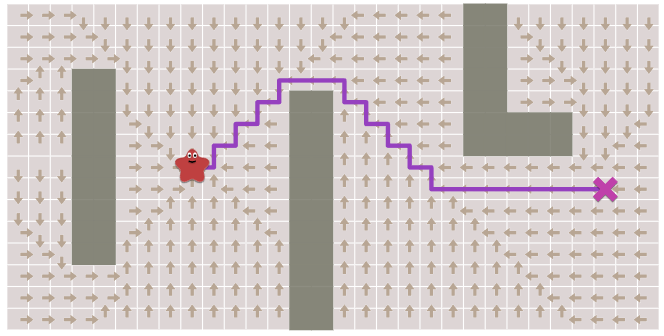
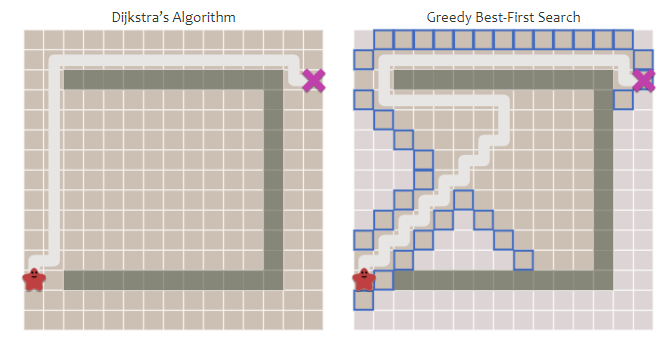
然而也带来一个问题,当存在障碍物的时候,这个方法用来导航会走弯路。
当然这是可行的,不过并不正确,我们结合上面这两种方法,就是A star算法。
A star A星算法同时考虑当前的花费和与目标的估计值,它的伪代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 PriorirtQueue<int> q; Hash<int> s; Hash<int> cost; q.push(start); s[start] = None; cost = 0; while(s.empty() == false) { currnet = s.pop(); if(current == goal) break; for(neighbors of current) { //Calculate new cost newcost = cost[current] + graph.cost(neighbors); if(s.contain(neighbors) == false || newcost < cost[neighbors]) { cost[neighbors] = newcost; //Changed here priority = newcost + heuristic(goal, next); q.push(neighbors, heuristic); s[neighbors] = current; } } }
A star算法同时将两种距离考虑进去,既不会像Dijkastra那样无目的地搜索,也不会想启发式方法那样找到非最短路径,它被认为是最好的路径搜索算法。