games101系列(5) 光线追踪
前言
前面的课程和作业中,我们熟悉了一套完整的光栅化过程,然后学习了一些典型的几何表示,现在来到课程的第三个部分,光线追踪。从渲染的角度来说,光栅化和光线追踪是两种不同的着色方式,前者通过光照模型对片段进行投影,然后得到片段颜色,是从物体颜色的计算再到像素;后者虽然是光照模型,但是完全改变了着色方法,从像素出发,模仿光线的传播,完整地计算片段经过光线折射、投射后得到的结果。
下面,我们简单介绍一下两种方法的优缺点,然后进入光线追踪的学习。
光栅化与光线追踪
光栅化总结
光栅化计算比较简单,将物体投影到屏幕上进行内外判断,决定片段颜色。
另外,光栅化做阴影的方法也有,就是Shadow Map,原理就是一个点如果不在阴影中,那么应该是从光源和摄像机视角都能看见的。具体做法是,从光源打光线到场景物体,得到一个含有每个像素的深度信息的Shadow Map,然后再从摄像机打光线到整个场景,这次计算每个像素(或片段)与光源的距离(转化到之前空间中,其实反过来也可以)作为深度值,然后映射(可能走样)找到Shadow Map中记录的值进行比较,如果这两个值相同,就说明该像素没有在阴影中;否则像素就在阴影中。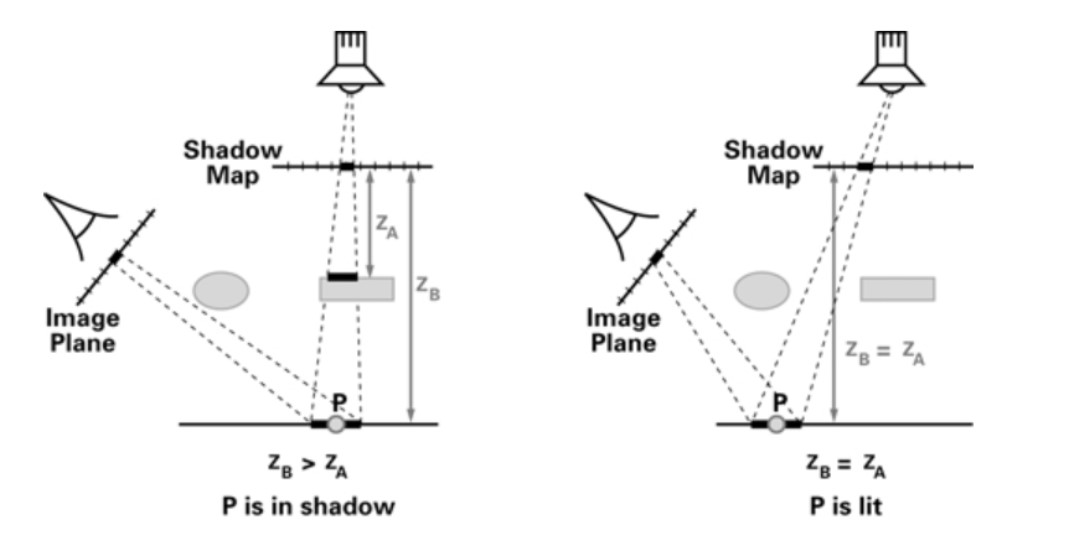
上面ZA就是光源记录的深度值,ZB是摄像机记录后,转换到光源空间中的值,ZB大于ZA表示ZB离光源更远,所以该点是光源不可见的,在阴影中。
这样,光栅化的基本方法就都介绍完了,最大的优点就是计算快,所以可以轻松做到实时计算,并且也有不错的效果。但是光栅化由于模型都是假设得到的,缺乏实际理论,导致光栅化的结果也很简单,一个是阴影是硬阴影,再一个是只模拟了局部光照,并没有光线多次反射的间接光照效果,也就是全局光照。
光线追踪优缺点
光线追踪的做法就跟名字一样,基本按照光学原理在场景中计算光线的弹射,模拟全局光照效果。优点当然是对全局光照效果的精确模拟,缺点也很明显,光线的多此计算是非常耗费计算量的,所以光线追踪不容易实时应用。
光线追踪
光线
要模拟光线传播,首先要定义光线的性质。在光线追踪中,光线就用射线表示,做如下假设:
- 光线沿直线传播;
- 光线之间不会发生碰撞;
- 光线从光源出发,经过反射、折射得到摄像机,并且这个过程可逆。
光线投射 Ray Casting
这个模型是80年代提出的,可以称为光线追踪的基本过程。先说一下基本的做法:
- 从摄像机出发,每个像素投射一根光线出去;
- 用投射的光线寻找光源,从而判断阴影。
也就是说,由于光线具有可逆性,所以从光源出发和从相机出发等效,从相机出发达到一个物体,这个物体就是相机可见;进一步,如果这个光线最终达到了光源,那么这个光源就不在阴影中,这样的一条光路包含的能量,就可以用来计算一个像素的颜色。现在,可以明确光线追踪的做法细节了。
针孔相机模型 Pinhold Camera Model
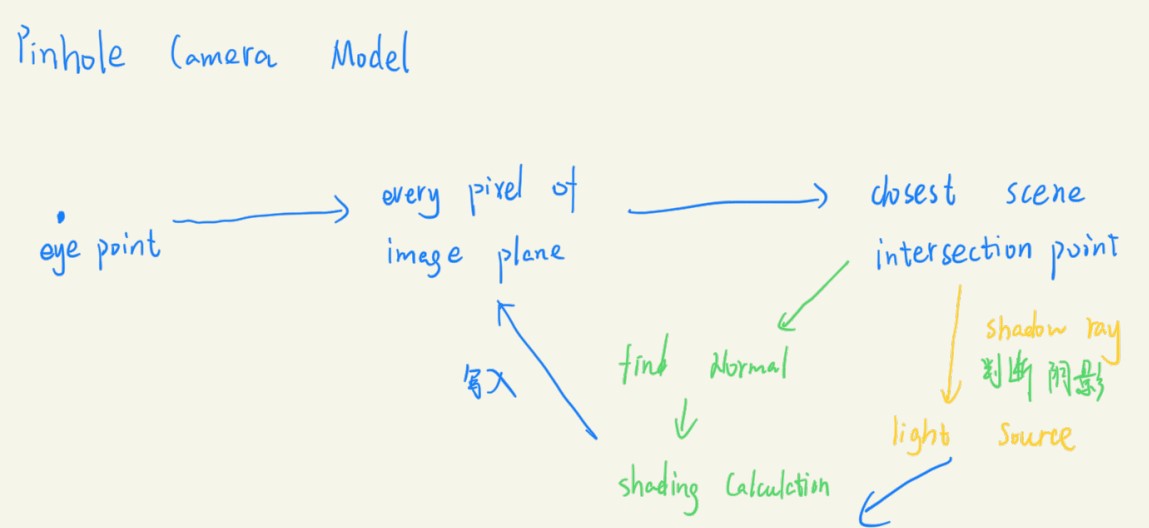
从观察点出发,对每个像素都进行光线投射,每根光线进行上面的操作:光线沿着光路找到第一个相交的物体点,对这个物体点找到法线进行着色计算(例如使用Phong光照模型),而且还要通过这个点能否达到光源(与光源是否有遮挡物,反过来看就是光线从光源出发没有到观察点)判断点是否在阴影中,然后综合阴影和着色结果,写入光线发出的像素中。
Witted-Style Ray Tracing (Recursive)
很显然,上面的模型虽然是通过光线进行追踪,但是仍然没有考虑光线弹射,所以得到的结果还是局部的光照。考虑通过递归的方式处理任何一根光线,如果光线发生了折射或者反射,那么以这个点为出发点重新计算光线的投射,这才是完整的光线追踪。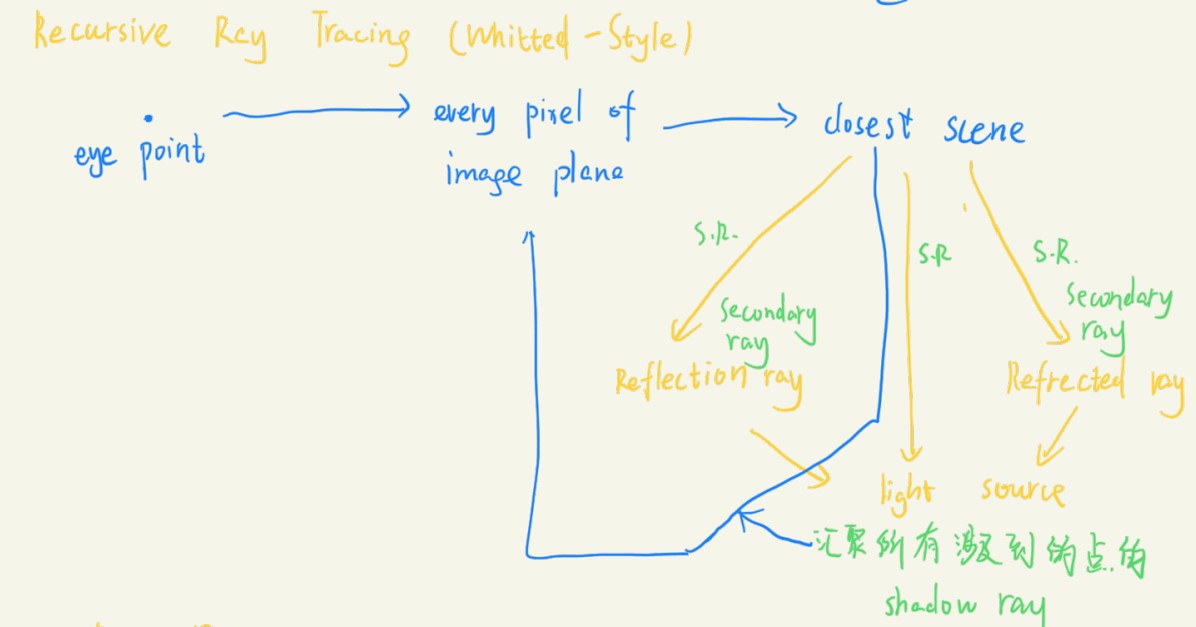
仍然从观察点出发,对每个像素投射光线,光线找到最近的相交点,并且考虑反射和折射光线(统称为Secondary Ray),如果发生了反射折射,就对反射折射光线进行递归;如果不发生(例如遇到漫反射材质),则停止追踪这条光线,对这个不发生发射折射的点使用其他光照模型得到着色结果,并返回颜色,最终在递归中汇聚所有值,平均到出发的像素中。
光线求交点
现在,给光线一个完整的数学定义: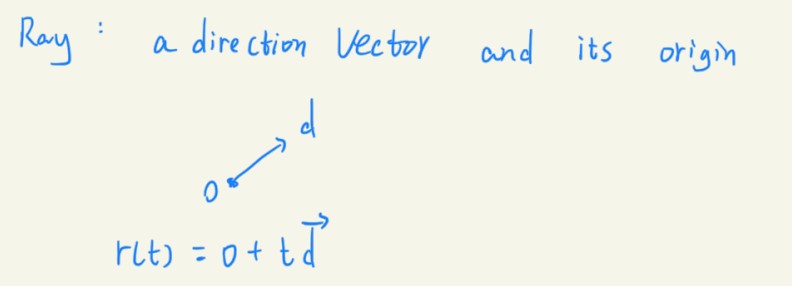
隐式表示的物体
然后,先考虑二维中光线与球相交的情况,球可以用隐式的公式表示,所以把两个方程联列求解: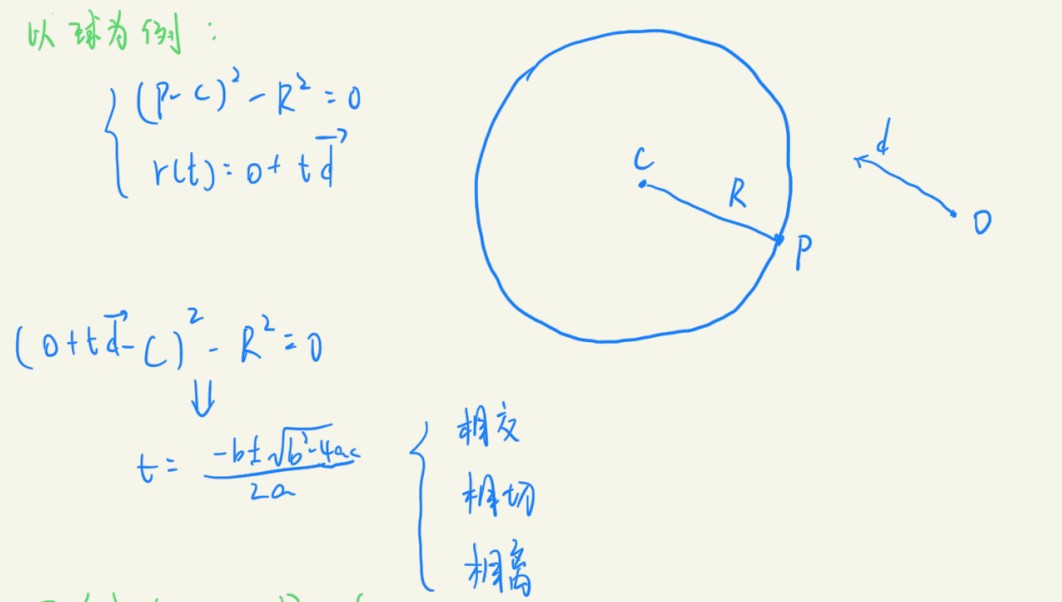
所以,可以使用相同的方法对三维中所有隐式表示f(p)=0,p点如果也可以用光线的方程表示,那么p就是交点。
显式表示的物体
显式表示的物体确定了点的坐标,其实也就确定了许多的三角形面,光线追踪中,我们先看光线与面的交点,再这个交点是否在面上的三角形内,如果两者都满足,才能确定一个交点。
普通方法
与面相交的交点是比较好求的,方便了计算过程。
其实也是隐式求交的方法,只不过是平面的函数表示。P点是平面上的点,P’是等待判断的点,如果P’在平面上,那么他和P点连成的向量应该和法线N垂直。最后解出t的表示如上,如果t是非负实数,说明这个点存在,带入光线的定义得到点坐标。
求出点的坐标后就是判断三角形内外了,采用前面的向量叉乘法,就可以得到判断结果。
Moller Trumbore Algorithm
这里介绍一种更快的方法,利用重心坐标的性质求解。
右边三个P向量表示三角形的三个顶点(不是向量),如果点在三角形内部,那么重心坐标的三个权重应该在[0,1]之间,秩为3的矩阵求解三个未知数,通过克莱默法则得到下面的解形式:
好了,现在知道了如何求交点,完成作业5以后,再进一步学习光线追踪。
作业
本次作业还是使用了新的框架,要求写的内容就是上面求交点的算法,还有最简单的光线追踪算法。首先我们分析光线追踪算法的具体实现。
光线追踪算法部分
作业要求为每一个像素生成一条对应的光线,调用castRay()函数得到颜色,并存储在帧缓冲区的相应像素中。阅读框架发现,实际上要做的只是求屏幕空间的像素对应到世界中的坐标,也就是说,这和之前光栅化之前的步骤都相同,而且已经得到了屏幕坐标系(NCD)中的像素坐标了。但是现在使用了不同的渲染方式,从像素出发,所以要重新计算片段原本在世界系中的位置,方便投射光线。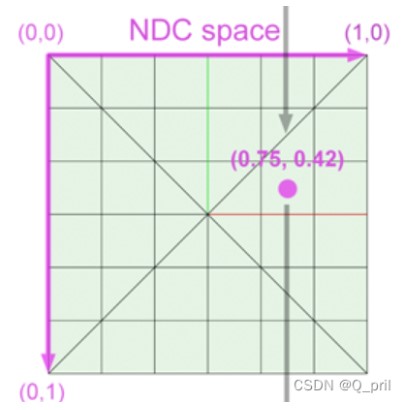
那么分析一下这些坐标的变换情况如下,世界坐标系中的原始坐标P0,经过透视投影压缩到[-1,1]的范围中,这是P1,这一步中定义了fov角和横纵比ratio,然后投射到屏幕上得到P2,范围是[0,+inf]。所以现在反过来已知P2求P0,首先要将P2重新压缩到[-1,1]上,对X坐标应该先除以屏幕宽度width,然后乘以2,减去1;Y坐标和X的计算相反,因为屏幕坐标系中Y正方向向下,所以我们是用负的Y坐标除以屏幕高度,乘以二然后加上1。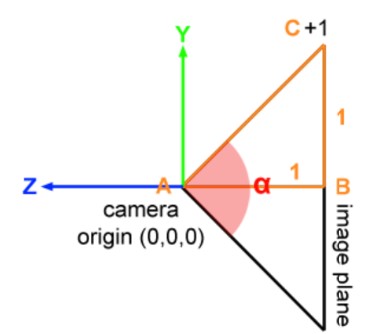
得到P1后,分析透视投影的fov角,tan(fov/2)=高宽/Z值,这实际上就是直接对XY坐标的缩放,所以框架给出了scale这个值放大坐标。最后,这样得到的XY坐标实际上是相等的,因为还有一个宽高比没有用,宽高比就是宽度是高度的多少倍,所以把X坐标乘以这个宽高比,就得到了原始的X坐标,Y坐标不用乘,这就是P0。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42void Renderer::Render(const Scene& scene)
{
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = std::tan(deg2rad(scene.fov * 0.5f));
float imageAspectRatio = scene.width / (float)scene.height;
// Use this variable as the eye position to start your rays.
Vector3f eye_pos(0);
int m = 0;
for (int j = 0; j < scene.height; ++j)
{
for (int i = 0; i < scene.width; ++i)
{
// generate primary ray direction
//(i+0.5,j+0.5)才是像素在屏幕上的位置,而且因为屏幕以左上角作为原点,
//导致y轴坐标向下为正方向,所以实际上y的计算和x相反
float x = (2 * (i + 0.5) / scene.width - 1) * imageAspectRatio * scale;
float y = (1 - 2 * (j + 0.5) / scene.height) * scale;
// TODO: Find the x and y positions of the current pixel to get the direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable *scale*, and
// x (horizontal) variable with the *imageAspectRatio*
Vector3f dir = normalize(Vector3f(x, y, -1)); // Don't forget to normalize this direction!
framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
}
UpdateProgress(j / (float)scene.height);
}
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}
只有中间求x,y那里是需要填写的,其他已经写好,不过记得对dir这个方向向量进行归一化。
三角形求交部分
这部分就很简单了,按照公式计算即可,向量和点都已经给出。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
const Vector3f& dir, float& tnear, float& u, float& v)
{
// TODO: Implement this function that tests whether the triangle
// that's specified bt v0, v1 and v2 intersects with the ray (whose
// origin is *orig* and direction is *dir*)
// Also don't forget to update tnear, u and v.
//按照克莱默法则得到的解形式计算就行了
Vector3f E1 = v1 - v0;
Vector3f E2 = v2 - v0;
Vector3f S = orig - v0;
Vector3f S1 = crossProduct(dir, E2);
Vector3f S2 = crossProduct(S, E1);
tnear = dotProduct(S2, E2) / dotProduct(S1, E1);
u = dotProduct(S1, S) / dotProduct(S1, E1);
v = dotProduct(S2, dir) / dotProduct(S1, E1);
if (tnear >= 0 && u >= 0 && v >= 0 && (1 - u - v) >= 0)
return true;
return false;
}
这里都是引用形式,所以直接修改变量名即可。如果解出的三个值都满足条件,t非负,重心坐标的三个权重都在0和1之间,那么点就在三角形内部。
结果
