games101系列(4) 几何
前言
第四次作业是几何部分的内容,课程中关于这部分讲了很多,比较庞杂,所以只选择了贝塞尔曲线简单实现。博客会回顾一下这部分的知识,然后给出作业效果。
几何概念
隐式表示
间接表示某些满足特定条件的点,例如公式表示f(x,y,z)=0。
隐式表示方法
- Algebraic Surface
- Constructive Solid Geometry
- Distance Functions
- Level Set Methods
- Fractals
优缺点
- 描述使用等式,比较简单;
- 查询简单,速度快;
- 计算光线容易
- 能够精确描述简单的物体
拓扑变换容易掌握;
但是不能描述复杂的形状。
显式表示
直接给出点的坐标,或者点坐标的查询方式。
显式表示方法
- 点云;
- 多边形面;
- wavefront obj,定义点和点的连接关系,纹理坐标,法线等。
优缺点
- 容易判断内外;
- 需要存储空间;
曲线
贝塞尔曲线
二次贝塞尔曲线

分段贝塞尔曲线

曲面
Subdivision
增加面数。
Loop Subvision
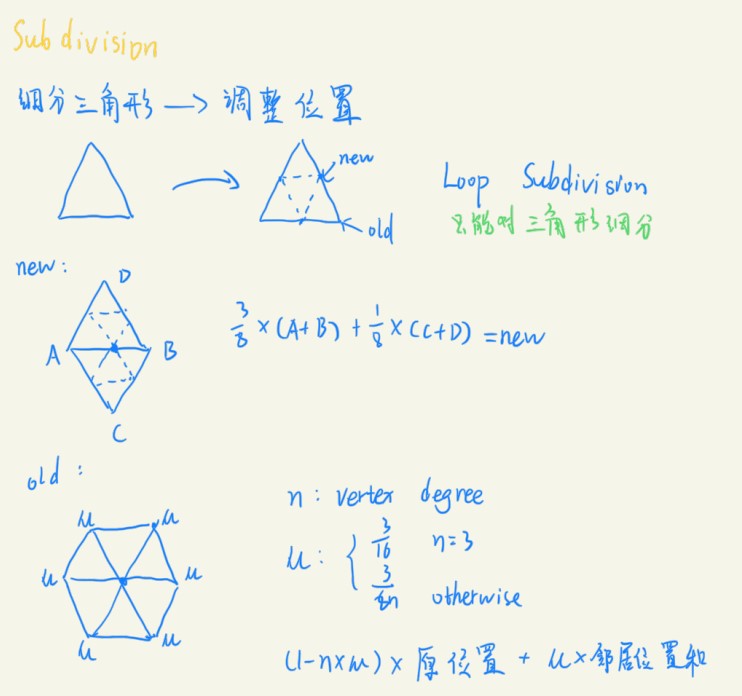
Catmull—Clark Subvision
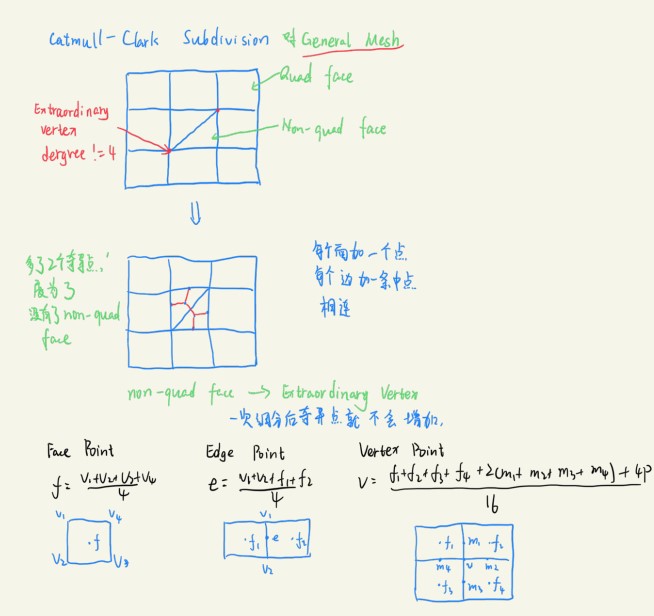
Simplification
减少面数。
Edge Collapsing & Quadric Error Metrics

Regularization
面数不变。
作业
作业4内容就是通过鼠标选择4个控制点,然后绘制贝塞尔曲线。框架直接给出了通过前面推导的二项式公式得出的贝塞尔曲线,也就是数学方法,现在我们要做的是通过几何方法得到正确的贝塞尔曲线。先看看数学方法得到的效果。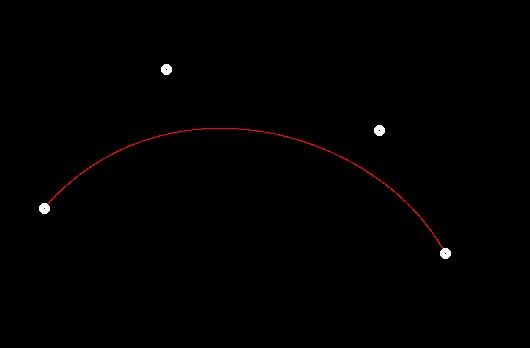
绘制的曲线是红色的,现在看看代码是怎样实现的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15void naive_bezier(const std::vector<cv::Point2f>& points, cv::Mat& window)
{
auto& p_0 = points[0];
auto& p_1 = points[1];
auto& p_2 = points[2];
auto& p_3 = points[3];
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 +
3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3;
window.at<cv::Vec3b>(point.y, point.x)[2] = 255;
}
}
函数作用是使用opencv在窗口中改变像素的颜色,所以没有返回值,输入一个是指定的控制点数组points,一个是用于绘制的opencv窗口句柄window。那么现在我们就知道绘制的方法了,先得到要绘制的点的坐标,然后仿照上面使用window.at方法指定。
作业要求实现两个函数,一个是Bezier函数,输入和作用与native_bezier完全相同,只是方法不同,要求对比例t进行迭代,增量微小,每次调用另一个函数recursive_bezier,返回当前t值对应的像素坐标。注意,这里按照要求要将曲线绘制成绿色,所以将像素的RGB中G赋值为255最大值。1
2
3
4
5
6
7
8
9
10
11
12void bezier(const std::vector<cv::Point2f>& control_points, cv::Mat& window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (double t = 0; t <= 1; t += 0.001)
{
auto point = recursive_bezier(control_points, t);
//下面之所以只赋值[1],是为了将曲线显示成绿色
//将y行x列的像素的Green值赋值为255
window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
}
}
再分析另一个,recursive_bezier函数就是使用之前介绍的算法,输入还是控制点,回顾算法过程,实际上是一个递归的过程,三个控制点的贝塞尔曲线,只需要递归一次,四个控制点的贝塞尔曲线,需要递归两次,从中发现一个规律,每递归一次,控制点减少一个,当控制点组points只剩下两个点的时候,按照t比例划分就能得到最后的结果了。所以递归结束的标志就是控制点只剩下两个的时候,将两个控制点的t比例分割点返回即可。1
2
3
4
5
6
7
8
9
10
11
12
13cv::Point2f recursive_bezier(const std::vector<cv::Point2f>& control_points, float t)
{
// TODO: Implement de Casteljau's algorithm
if (control_points.size() == 2)
return control_points[0] + t * (control_points[1] - control_points[0]);
std::vector<cv::Point2f> ano_points;
for (int i = 0; i < control_points.size() - 1; i++)
{
ano_points.push_back(control_points[i] + t * (control_points[i + 1] - control_points[i]));
}
return recursive_bezier(ano_points, t);
}
这部分函数是参照网上写的,因为我起初没有详细看框架,一些方法不知道怎么用,所以这里建议自己写的时候都看一看框架。现在调用自己编写的函数,得到下面的结果。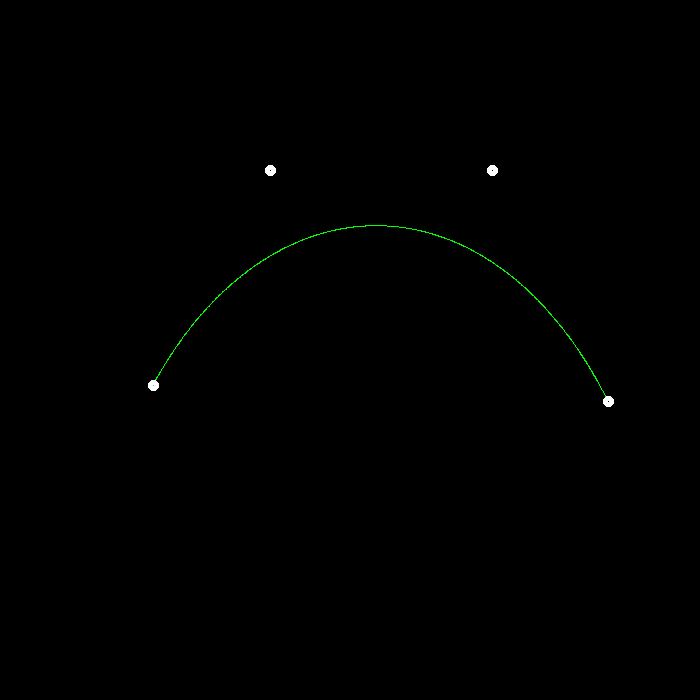
最后根据作业要求,同时调用Bezier和native_bezier,得到曲线颜色应该是(255,255,0),也就是黄色,这就说明自己编写的函数是正确的。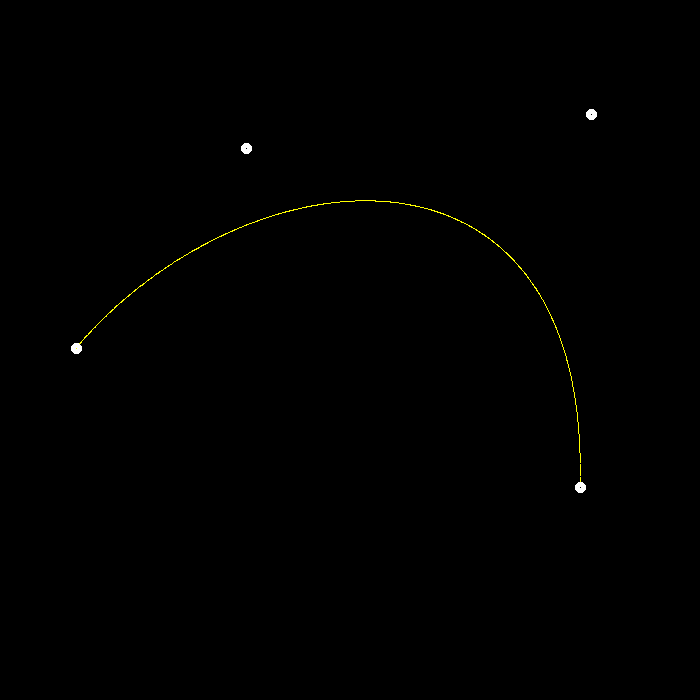
反走样
有机会以后再做,作业要求里有注释。