games101系列(2) 三角形的光栅化
前言
前面说到,在渲染管线中顶点流首先经过MVP变换,得到一个标准立方体(canonical cubic),但是显然不能将这个立方体直接显示到屏幕上,而是要将这个立方体压到屏幕上,从而给每个像素赋值,这一步就是光栅化。当然,将立方体压到屏幕上这个过程显然是在对Z轴上的坐标进行处理,在这之前还需要先处理一下X,Y轴坐标,这就是视口矩阵的作用。
现在我们先介绍视口矩阵,然后再关注三角形的光栅化。
视口矩阵
标准立方体是通过某种投影,将顶点坐标变换到标准立方体空间中得到的结果,这个立方体包含了所有我们需要表示的物体。而现在要处理各个物体的XYZ坐标,符合屏幕大小,并且还要通过某种方式来做出物体遮挡的效果。直观地来想,调整到屏幕大小应该是在XY轴上处理,遮挡应该是在Z轴上处理,所以先处理XY轴,通过视口矩阵让XY坐标放大,计算出屏幕坐标,再思考如何处理Z轴。
上一节求出的标准立方体,坐标范围都在[-1,1]之间,实际上视口矩阵的处理也很简单,因为屏幕坐标规定的范围分别是[0,width]和[0,height],所以想到之前的线性变换,只需要一个平移和一个缩放,也就是一次仿射变换,就能得到需要的屏幕坐标了。
首先对坐标进行一次缩放,标准立方体的X,Y轴长度都是2,等比例放大到width和height,也就是变成原来的width/2和height/2倍,接着都向正方向平移一半的长度,就将起始位置变换到(0,0)。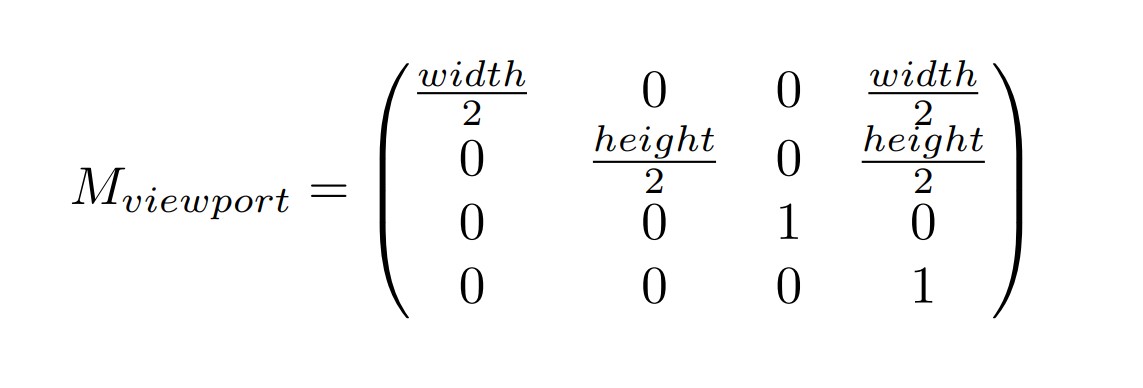
现在可以总结一下顶点坐标的变换了,一个物体的顶点流,先经过(MVP变换)模型视图变换,投影变换,得到标准立方体(canonical cubic),然后还要经过视口变换,将裁剪坐标系中的XY坐标变换到屏幕坐标系,与Z坐标进入光栅化过程。
光栅化
光栅化的真正原因是受限于硬件的像素排布,我们会给每个像素计算一个颜色用于显示,而每个像素显示怎样的颜色,才是要解决的问题。
这时就需要用到前面的处理的坐标了,通过采样的方式,我们判断每个像素在什么物体的面上,根据物体的颜色给像素赋值,建立一种映射关系。下图是2D平面的三角形光栅化例子。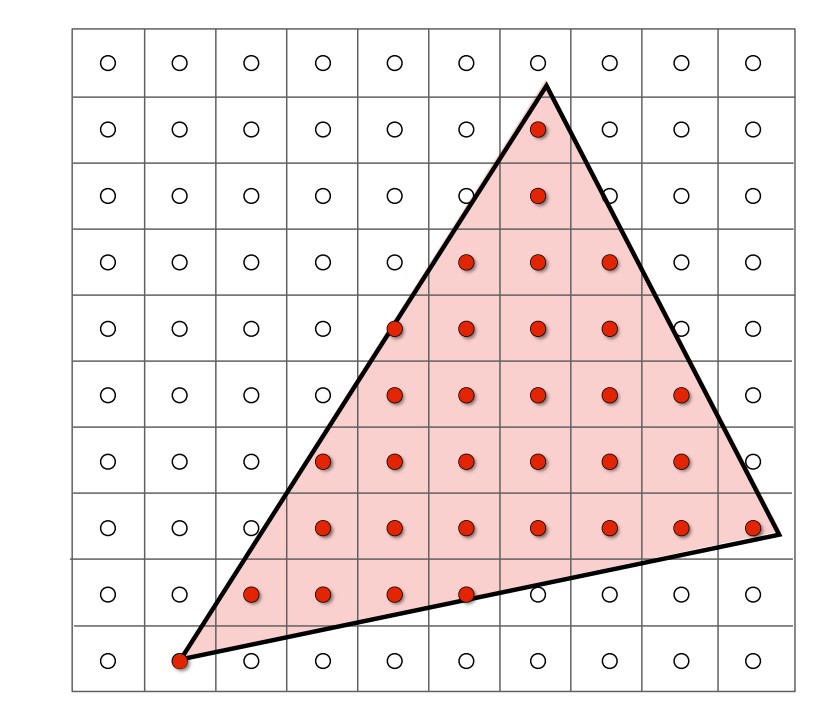
显然,判断一个像素点是否在这个三角形内部是非常必要的。下面的算法假设像素大小为1*1,平面最左下角坐标为(0,0)。
判断点在三角形内部
这里使用的方法是判断向量叉积,只要一个点在三角形内部,那么从三个顶点到该点连线的向量,与顺序连接三个顶点得到的边向量,他们分别的乘积,一定是同号的。否则,一定会有异号的结果。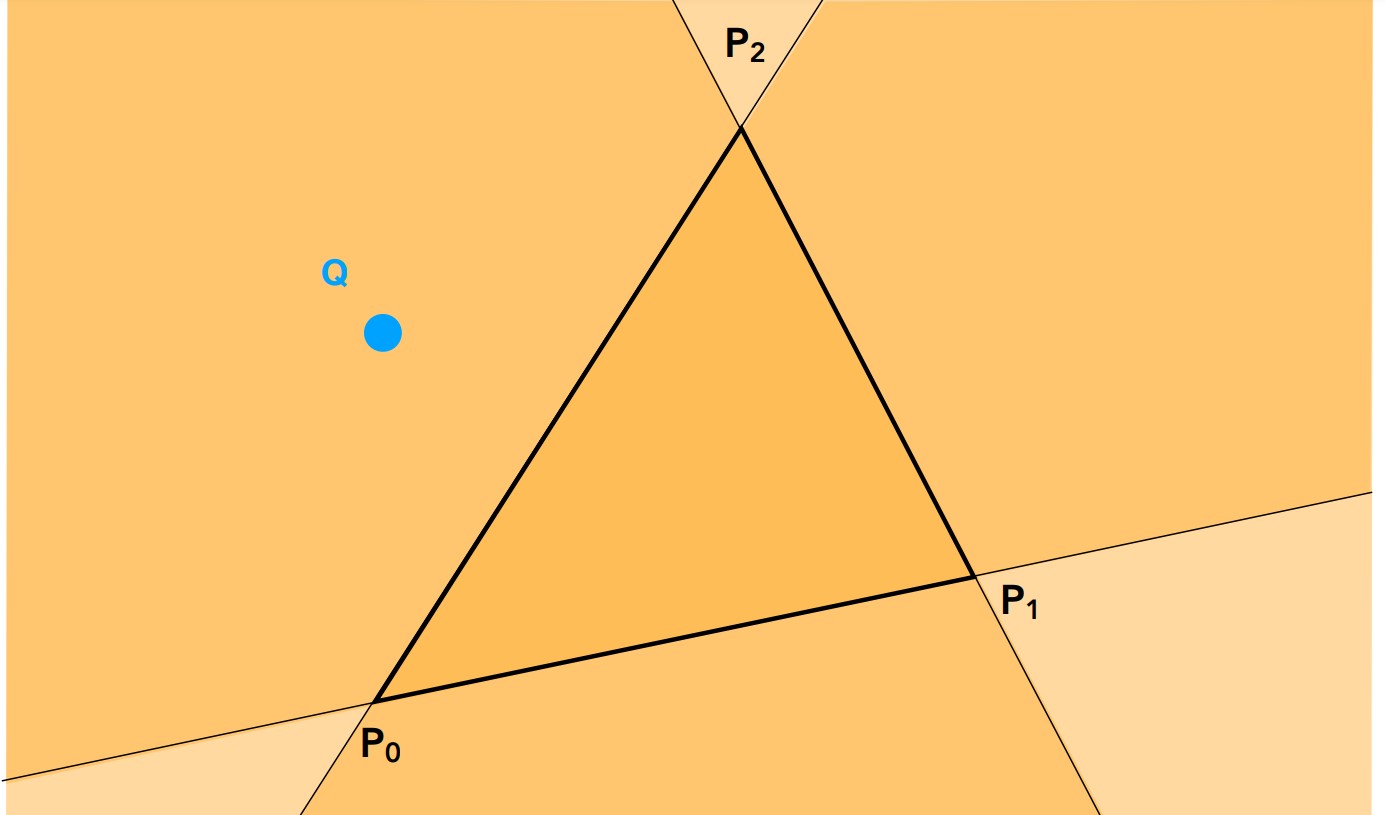
如图顺时针连接P0,P1,P2,得到向量P0P1,P1P2,P2P0,同时连接指向Q点的三个向量P0Q,P1Q,P2Q,计算叉积P0P1与P0Q>0,P1P2与P1Q>0,P2P0与P2Q<0,因此判断Q在三角形外部。
bouding box
为了减少需要计算的像素点,采用包围盒是很有用的措施,利用三角形三个顶点可以求出一个包围三角形的长方体如下,只需要计算包围盒中的像素即可,因为包围盒外部的像素不可能在三角形中。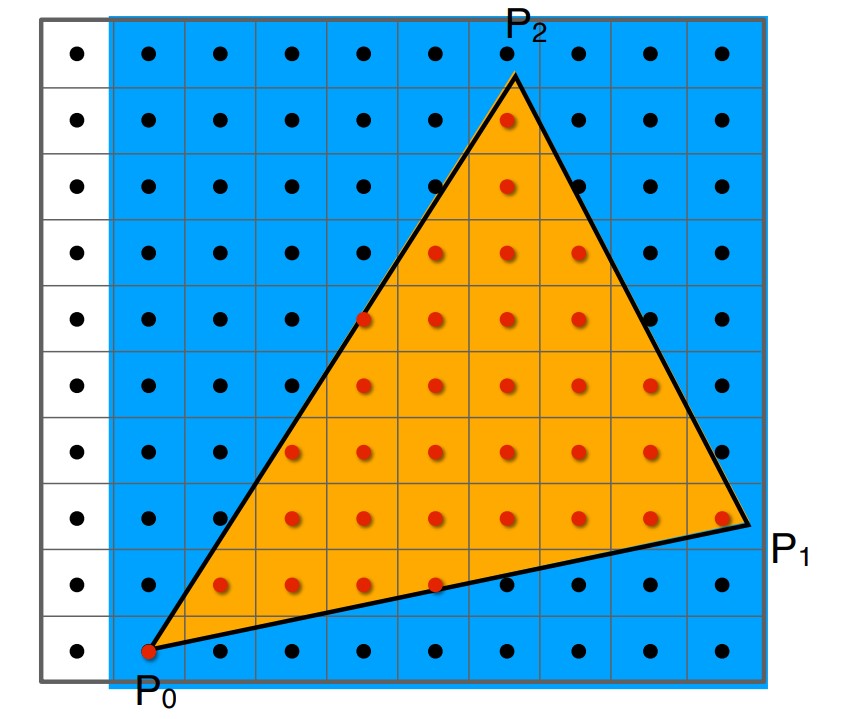
抗锯齿
锯齿的产生是因为采样率低(低分辨率)导致的信号混叠,详细原理涉及频域和时域的傅里叶变换,这部分可以看课程理解,不理解也可以直观感受抗锯齿或者反走样的做法。
前面光栅化得到的三角形与实际看到的三角形差别很大,就是因为锯齿的存在。而反走样也有一些方法,最简单的是低通滤波器,用这个卷积核将图形中的高通滤波过滤,就得到模糊的样本,在一定程度上消除锯齿,使其同样变得模糊。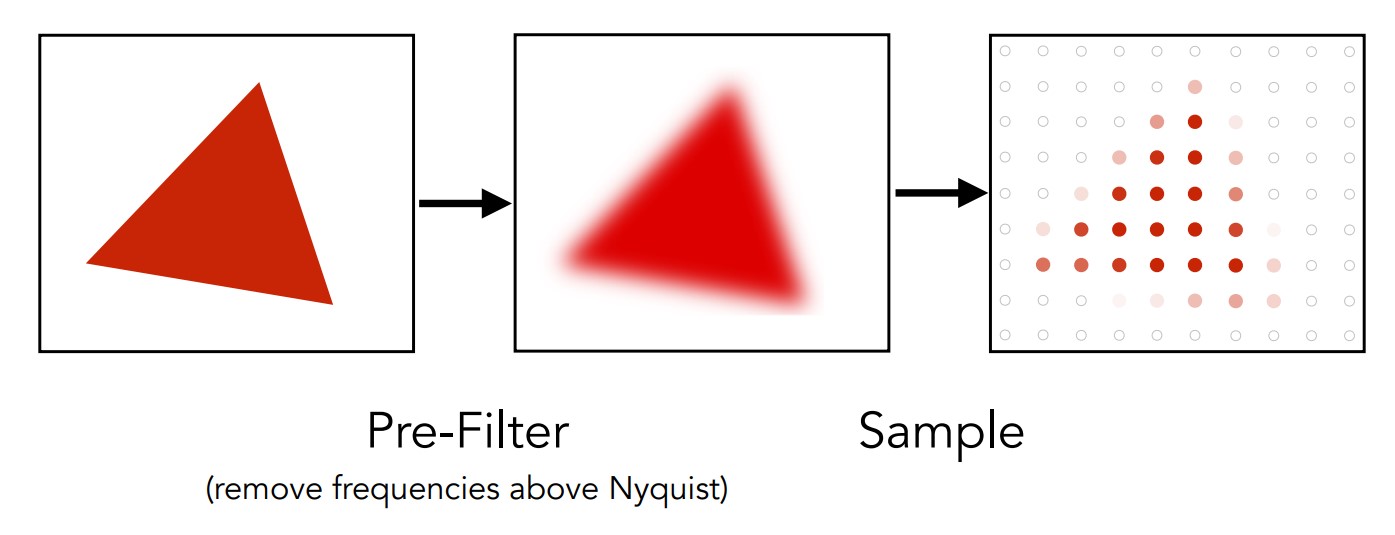
还有一个方法叫超采样(MSAA),增加采样频率,将每个像素分成很多个像素采样,最后平均像素中子像素得到的结果。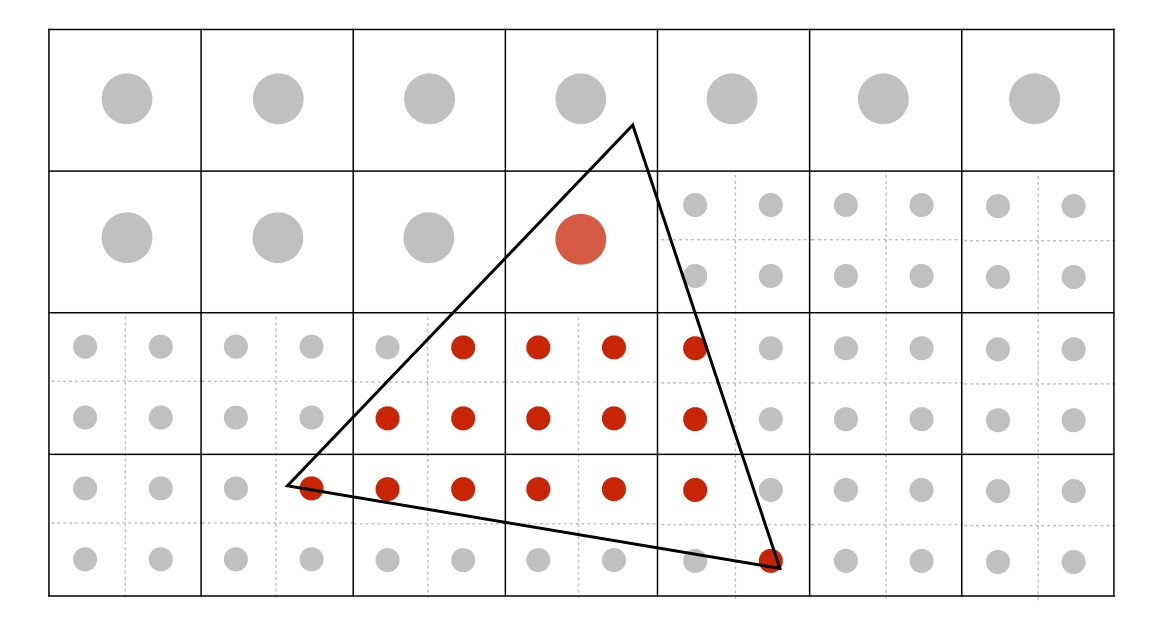
当然还有很多反走样技术,稍后的作业2中会实现MSAA反走样,作为入门。
深度测试
现在来解决前面留下的Z轴坐标,物体的遮挡关系显然是要通过Z轴坐标来判断,离摄像机近的物体才能被显示到平面上,因此设计一个缓冲区,也就是Z—Buffer来判断,在之前遍历像素的过程中,如果发现了物体某个点有更靠近平面的Z值,就将这个对应像素的值更新为靠近平面的点的值。
作业2
作业2要实现一个三角形的光栅化过程,其中我们需要编写的是三角形bounding box求解的函数,以及判断三角形内部的Inside函数,当然还有深度测试即像素更新。
三角形光栅化函数
我们从基本的光栅化开始,要绘制的物体只有两个固定的三角形,所以要先设计函数求三角形的包围盒,然后遍历包围盒中的像素,进行深度测试,并更新深度缓存中的深度值和对应像素的颜色,最后得到正确的渲染结果。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38void rst::rasterizer::rasterize_triangle(const Triangle& t)
{
auto v = t.toVector4();//返回顶点的齐次坐标形式
// TODO : Find out the bounding box of current triangle.
int box_l, box_r, box_b, box_t;
box_l = static_cast<int> (std::min(v[0].x(), std::min(v[1].x(), v[2].x())));
box_r = static_cast<int> (std::max(v[0].x(), std::max(v[1].x(), v[2].x())));
box_b = static_cast<int> (std::min(v[0].y(), std::min(v[1].y(), v[2].y())));
box_t = static_cast<int> (std::max(v[0].y(), std::max(v[1].y(), v[2].y())));
// iterate through the pixel and find if the current pixel is inside the triangle
for (int i = box_l; i <= box_r; i++)
{
for (int j = box_b; j <= box_t; j++)
{
// If so, use the following code to get the interpolated z value.
if (insideTriangle(i + 0.5, j + 0.5, t.v))
{
float alpha, beta, gamma;
std::tie(alpha, beta, gamma) = computeBarycentric2D(static_cast<float>(i + 0.5), static_cast<float>(j + 0.5), t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
if (depth_buf[get_index(i, j)] > -z_interpolated)
{
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
depth_buf[get_index(i, j)] = -z_interpolated;
Eigen::Vector3f point;
point << static_cast<float>(i), static_cast<float>(j), -z_interpolated;
set_pixel(point, t.getColor());
}
}
}
}
}
求解包围盒很简单,找到三角形坐标的四个最值并记录,要记得转换为整型变量,因为像素是以1为单位长度的,就像课程中假设的那样。然后,直接根据这个坐标开始遍历,对象是用i为横坐标,j为纵坐标表示的像素,如果该像素在传入的三角形当中(使用下面编写的函数判断,而且所有坐标都转换到屏幕空间了),那么先计算该坐标位置的深度插值(利用三角形重心坐标,只需要知道顶点就可以计算任意位置的深度值),并比较当前深度缓存中该像素的深度,如果这个深度值小于当前深度缓存值,说明现在找到一个更靠近屏幕的点,应该优先显示,所以更新深度缓存的值,同时也更新该像素的颜色,就完成了一次遍历的过程。
值得说明的是,网上有博客指出Z值并没有反转,所以如果你直接使用原本的Z值,得到的结果正好与作业说明相反,是下面这个样子: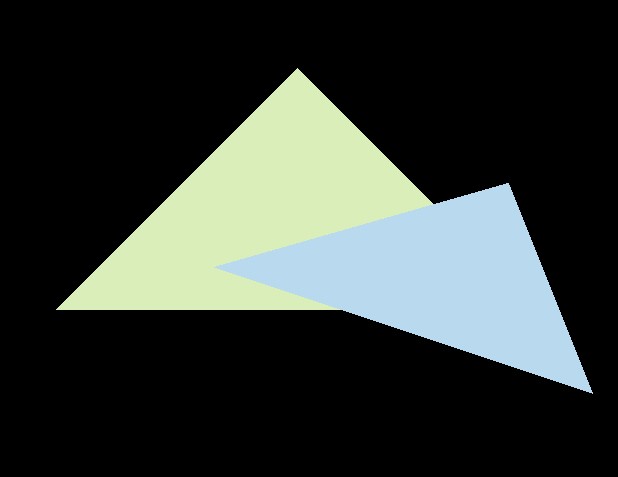
所以,要得到和他相同的结果,实际上需要手动将得到的Z轴插值取反,这就是上面负号的由来了。最终得到的效果是这样: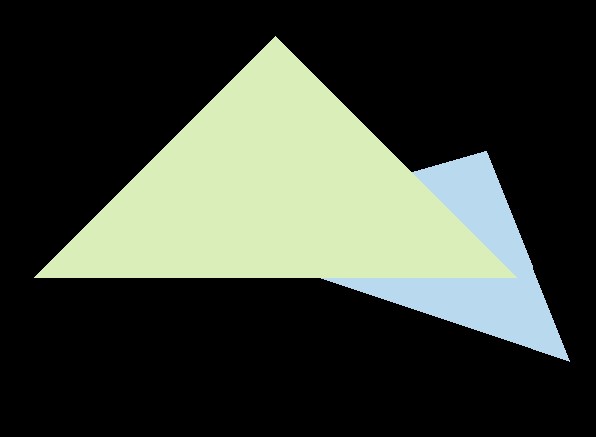
另外,如果将大于改成小于,而不改变符号,那么得到的是全黑的窗口,这显然是因为完全没有更新过,说明深度缓存的初始值是一个很大的正值。在代码中可以找到,clear函数中会将深度值赋值为正无穷Infinity。
现在再从上面的基础上实现2*2的MSAA抗锯齿。根据前面介绍的原理,现在修改一下像素个数和像素坐标,将原来的每个像素划分为四块即可,然后根据这四个子像素在三角形中的个数,然后决定颜色的比例。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51void rst::rasterizer::rasterize_triangle(const Triangle& t)
{
auto v = t.toVector4();//返回顶点的齐次坐标形式
// TODO : Find out the bounding box of current triangle.
int box_l, box_r, box_b, box_t;
box_l = static_cast<int> (std::min(v[0].x(), std::min(v[1].x(), v[2].x())));
box_r = static_cast<int> (std::max(v[0].x(), std::max(v[1].x(), v[2].x())));
box_b = static_cast<int> (std::min(v[0].y(), std::min(v[1].y(), v[2].y())));
box_t = static_cast<int> (std::max(v[0].y(), std::max(v[1].y(), v[2].y())));
std::vector<Eigen::Vector2f> position{
{0.25, 0.25},
{0.75, 0.25},
{0.25, 0.75},
{0.75, 0.75}
};
// iterate through the pixel and find if the current pixel is inside the triangle
for (int i = box_l; i <= box_r; i++)
{
for (int j = box_b; j <= box_t; j++)
{
int count = 0;
for (int index = 0; index < 4; index++)
{
if(insideTriangle(position[index].x() + i, position[index].y() + j, t.v))
count++;
}
// If so, use the following code to get the interpolated z value.
if (count > 0)
{
float alpha, beta, gamma;
std::tie(alpha, beta, gamma) = computeBarycentric2D(static_cast<float>(i + 0.5), static_cast<float>(j + 0.5), t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
if (depth_buf[get_index(i, j)] > -z_interpolated)
{
// TODO : set the current pixel (use the set_pixel function) to the color of the triangle (use getColor function) if it should be painted.
depth_buf[get_index(i, j)] = -z_interpolated;
Eigen::Vector3f point;
point << static_cast<float>(i), static_cast<float>(j), -z_interpolated;
set_pixel(point, t.getColor() * (count / 4.0));
}
}
}
}
}
可能采样数较少,这里看着还是不太明显。算法上改变的并不多,详细步骤是对每个像素计算子像素的四个坐标,只要有一个子像素在三角形中,就进入if更新,并且根据子像素在三角形中的比例调整颜色百分比,从而实现”模糊”的效果。
三角形内部函数
方法和前面介绍的一样,三个叉积符号判断是否在内部,这里选择的边向量是逆时针连接,那么根据右手定则,在内部时结果都为正,所以只要有一个结果为负数,就说明不在三角形内部。
这里注意作业的说明,将Z值做了反转,保证都是正值,也就是说本来框架中屏幕向里才是Z轴的负方向,屏幕向外是Z轴的正方向,所以前面判断叉积结果为正没有问题(根据右手定则拇指朝外)。而且两个二维向量的叉积,实际上是两个第三维为0的三维向量进行叉积,按照右手系标准确定方向,计算结果确定正负,所以直接通过数值判断也是正确的。
1 | static bool insideTriangle(int x, int y, const Vector3f* _v) |
可能由于Eigen的cross函数只支持三维向量的计算,所以如果用二维向量,需要手动用公式进行计算,否则可能编译错误;使用三维向量,只需要将第三维设置成0即可。