数据结构与算法复习(2)线性表
前言
本章介绍线性表,包括顺序表示和链式表示,要熟练掌握,要能写出最优性能。要注意动手编写代码。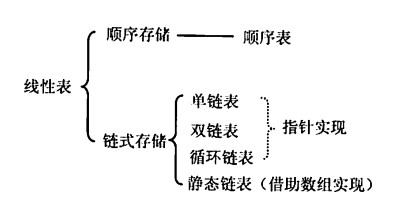
定义和基本操作
定义
线性表是具有相同数据类型的n个数据元素的有限序列,n为表长,n = 0时表为空表。
线性表有唯一一个表头元素和唯一一个表尾元素,且除表头元素外,每个元素都有且仅有一个前驱;除表尾元素外,每个元素都有且仅有一个后继。
线性表是逻辑结构,表示元素间一对一的相对关系。顺序表和链表是存储结构。
基本操作
1 | InitList(&L) |
顺序表
定义
线性表的顺序存储就是线性表,用地址连续的存储单元依次存储数据元素,使逻辑上相邻的两个元素在物理位置上也相邻,位置称为位序,从1开始。
特点是逻辑顺序和物理顺序相同。是一种随机存取的存储结构,一般用数组表述,空间可以静态分配也可以动态分配。
静态/动态分配空间指的是分配内存的大小是否能变化,本质上还是顺序存储。
操作
建表
1 | //静态分配 |
1 | //动态分配,一旦数据空间占满,就申请一块更大的空间替换现有空间。 |
ListInsert
1 | bool ListInsert(SqList &L, int i, ElemType e) |
时间复杂度n/2;
ListDelete
1 | bool ListDelete(SqList &L, int i, ElemType &e) |
时间复杂度(n-1)/2。
LocateElem
1 | LocateElem(SqList L, ElemType e) |
时间复杂度(n+1)/2。
链表
单链表
线性表的链式存储叫单链表,通过一组任意的存储单元来存储线性表中的数据元素,在每个结点存放指向后继的指针。
由于物理地址不相邻,所以插入删除元素不用进行移动,但同时也不能随机存取了。
使用头指针来标识一个单链表,头指针为NULL则表空。还可以在第一个结点之前增加一个头结点,优点是:1)方便处理第一个元素,统一所有元素的增删操作;2)方便处理空表,因为头结点非空,只要判断指针域即可,统一空表和非空表的。
操作
1 | typedef struct LNode{ |
头插法建表
1 | //注意这里用了引用传递的特性,下面会将参数解释成一个指向该类型的const指针,且指针指向的链表可以被修改,避免值传递的复制行为。 |
尾插法建表
1 | LinkList List_TailInsert(LinkList &L) |
GetElem
1 | LNode* GetElem(LinkList L, int i) |
LocateElem
1 | LNode* LocateElem(LinkList L, ElemType e) |
ListInsert
1 | bool ListInsert(LinkList L, int i, ElemType e) |
ListDelete
1 | bool ListDelete(LinkList L, int i) |
Length
1 | int Length(LinkList L) |
双链表
相比于单链表,双链表设置两个指针分别指向结点的前驱和后继,这样在寻找结点前驱的时候就不用从头开始遍历。1
2
3
4typedef struct DNode{
ElemType data;
struct DNode* prior, * next;
}DNode, *DLinkList;
ListInsert
在p指向的结点后插入元素。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19bool ListInsert(DLinkList L, DNode* p, ElemType e)
{
if(p == NULL)
return false;
DNode* s = (DNode*)malloc(sizeof(DNode));
s->data = e;
if(p->next == NULL)
{
s->next = p->next;
p->next = s;
s->prior = p;
return true;
}
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;
return true;
}
ListDelete
删除p指向的结点的后继。1
2
3
4
5
6
7
8bool ListDelete(DLinkList L, DNode* p)
{
if(p == NULL || P->next == NULL)
return false;
p->next = p->next->next;
p->next->next->prior = p;
free(p->next);
}
循环链表
循环单链表
单链表的尾结点后继指针指向头结点。表中没有为NULL的指针,通过判断头结点后继是否是头结点判断表空。而且因为已经成环,所以不用判断表尾,在每个位置上的插入删除都是等价的。
循环双链表
同理将双链表的尾结点后继指向头结点,头结点前驱指针也指向尾结点,就构成了循环双链表。
有时对单链表所做的操作通常在表头表尾,这时可以通过仅设置尾指针来优化,这样对头尾结点的操作都是统一的,且时间复杂度都是常数级。
静态链表
借助数组来表述线性表的链式存储结构,结点也有数据域data和指针域next,不过这里的指针是相对地址,称为游标。需要预先分配一块连续的内存空间。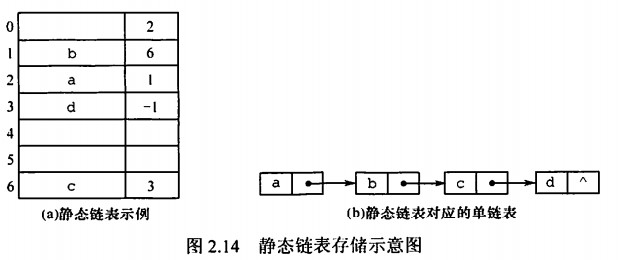
1
2
3
4
5#define MaxSize 50
typedef struct{
ElemType data;
int next;
}SLinkList[MaxSize];
以next为-1结束链表,通常使用在不支持指针的语言中。
顺序表和链表比较
存取方式
顺序表可以顺序存取,也可以随机存取;链表只能顺序存取;
逻辑结构和物理结构
顺序存储时逻辑地址相邻的元素物理地址也相邻,链式存储时逻辑地址相邻的元素物理地址不一定相邻。
查找、插入、删除操作
按值查找,顺序表和链表时间复杂度都为O(n),顺序表如果有序可以用折半查找降低;
按序查找,顺序表随机访问O(n),链表O(n);
插入,删除操作,顺序表要移动一定表长的元素,而链表只需要修改对应指针;
空间分配
顺序存储,如果采用静态存储分配,不灵活,可能会溢出;采用动态分配,又需要移动大量元素,而且可能分配失败;
链式存储,只在需要的时候申请分配,比较灵活高效。
存储结构的选择
存储上,如果线性表规模难以估计,用链式存储;
运算上,对于访问元素,按序访问使用顺序存储,按值访问区别不大;对于插入删除,表比较大的时候使用顺序存储很不方便,要移动的规模太大了,链表虽然要查找,但是操作更方便。
环境上,顺序表更容易实现,链表需要指针支持。
通常,稳定的线性表使用顺序存储,频繁插入删除使用链式存储。